题目内容
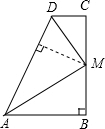如图，AB⊥BC，CD⊥BC，M是BC上的一点，连接DM、AM，且AM、DM分别平分∠DAB和∠ADC，试判断BM和CM的大小关系，并说明理由．考点：角平分线的性质
专题：
分析：过点M作MN⊥AD于N，根据角平分线上的点到角的两边距离相等可得BM=MN，CM=MN，然后求解即可．
解答：
解：如图，过点M作MN⊥AD于N，
∵AM、DM分别平分∠DAB和∠ADC，AB⊥BC，CD⊥BC，
∴BM=MN，CM=MN，
∴BM=CM．
解：如图，过点M作MN⊥AD于N，∵AM、DM分别平分∠DAB和∠ADC，AB⊥BC，CD⊥BC，
∴BM=MN，CM=MN，
∴BM=CM．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
多项式
的最高次项的系数是（ ）
| 2-x2 |
| 5 |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
如图所示，P是∠AOB的角平分线OC上的一点，PD⊥OA，PE⊥OB，垂足分别为D、E，则图中全等三角形有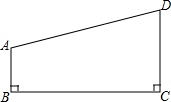
如图，已知在梯形ABCD中，AB∥CD，∠B=90°，AB=3，BC=11，DC=6，P为BC边上一点，使得△ABP与△PCD相似，求BP的长及△ABP与△PCD的面积比．