题目内容
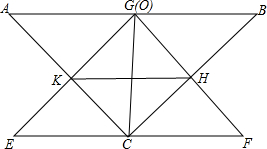 如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.
如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.(1)请判断△OHK的形状;
(2)求证:BH+AK=AC.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据等腰直角三角形和自己三角形的性质求出∠A=∠B=45°,∠ACG=∠BCG=45°,AO=BO=CO,CO⊥AB,求出∠BOC=∠KOH=90°,∠BOH=∠HOC,证△BOH≌△COK,推出BH=CK,OH=OK即可;
(2)根据BH=CK,即可得出答案.
(2)根据BH=CK,即可得出答案.
解答:(1)解:△OHK的形状是等腰直角三角形,
理由是:∵在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,
∴∠A=∠B=45°,∠ACG=∠BCG=45°,AO=BO=CO,CO⊥AB,
∴∠BOC=∠KOH=90°,
∴∠BOH=∠HOC=90°-∠AOK,
在△BOH和△COK中,
,
∴△BOH≌△COK(ASA),
∴BH=CK,OH=OK,
∵∠KOH=90°,
即△OHK的形状是等腰直角三角形;
(2)证明:∵BH=CK,
∴AC=AK+CK=AK+BH,
即BH+AK=AC.
理由是:∵在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,
∴∠A=∠B=45°,∠ACG=∠BCG=45°,AO=BO=CO,CO⊥AB,
∴∠BOC=∠KOH=90°,
∴∠BOH=∠HOC=90°-∠AOK,
在△BOH和△COK中,
|

∴△BOH≌△COK(ASA),
∴BH=CK,OH=OK,
∵∠KOH=90°,
即△OHK的形状是等腰直角三角形;
(2)证明:∵BH=CK,
∴AC=AK+CK=AK+BH,
即BH+AK=AC.
点评:本题考查了全等三角形的性质和判定,等腰直角三角形的性质和判定,直角三角形斜边上的中线性质的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
下列说法错误的是( )
| A、最大的负整数为-1 |
| B、倒数等于它本身的数有±1,0 |
| C、绝对值最小的有理数是0 |
| D、正数的相反数是负数 |
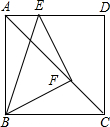 如图,已知正方形ABCD,在AD、AC上分别取E、F两点,使ED:AD=2FC:AC,求证:△BEF是等腰直角三角形.
如图,已知正方形ABCD,在AD、AC上分别取E、F两点,使ED:AD=2FC:AC,求证:△BEF是等腰直角三角形.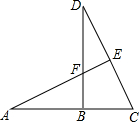 如图,已知BD⊥AC,AE⊥CD,BF=BC,求证:AF=CD.
如图,已知BD⊥AC,AE⊥CD,BF=BC,求证:AF=CD.