题目内容
2.已知关于x的方程(1+k)x2-(2k-1)x+k-1=0有两个不相等的实数根.(1)求k的取值范围;
(2)若α、β是方程(1+k)x2-(2k-1)x+k-1=0的两个不相等的实数根,试求2α+2β-3α•β的值.
分析 (1)由关于x的方程(1+k)x2-(2k-1)x+k-1=0有两个不相等的实数根,即可得△>0且1+k≠0,解此不等式组即可求得答案;
(2)由α、β是方程(1+k)x2-(2k-1)x+k-1=0的两个不相等的实数根,根据根与系数的关系,可得α+β=-$\frac{-(2k-1)}{1+k}$=$\frac{2k-1}{1+k}$,α•β=$\frac{k-1}{1+k}$,继而求得答案.
解答 解:(1)∵关于x的方程(1+k)x2-(2k-1)x+k-1=0有两个不相等的实数根,
∴△=b2-4ac=[-(2k-1)]2-4×(1+k)×(k-1)=-4k+5>0,
∴k<$\frac{5}{4}$,
∵1+k≠0,
∴k≠-1,
∴k的取值范围为:k<$\frac{5}{4}$且k≠-1;
(2)∵若α、β是方程(1+k)x2-(2k-1)x+k-1=0的两个不相等的实数根,
∴α+β=-$\frac{-(2k-1)}{1+k}$=$\frac{2k-1}{1+k}$,α•β=$\frac{k-1}{1+k}$.
∴2α+2β-3α•β=2(α+β)-3α•β=2×$\frac{2k-1}{1+k}$-3×$\frac{k-1}{1+k}$=$\frac{4k-2}{1+k}$-$\frac{3k-3}{1+k}$=$\frac{4k-2-3k+3}{1+k}$=$\frac{k+1}{1+k}$=1.
点评 此题考查了根的判别式以及根与系数的关系.注意△>0?方程有两个不相等的实数根;x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
15.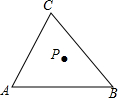 如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
 如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )| A. | ∠A,∠B的平分线的交点处 | |
| B. | AB的垂直平分线与∠B的平分线的交点处 | |
| C. | BC的垂直平分线与∠A的平分线的交点处 | |
| D. | AB,BC的垂直平分线的交点处 |
10.若关于x的一元二次方程(m-1)x2-2x+1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m<2且m≠1 | B. | m>2 | C. | m<-2 | D. | m<2 |
7. 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )| A. | 4 | B. | -4 | C. | ±4 | D. | -5 |
11.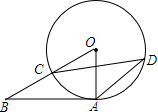 如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )
如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )
 如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )
如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )| A. | 27° | B. | 34° | C. | 36° | D. | 54° |
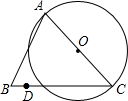 如图,等边三角形ABC的边长为10,以AC为直径作⊙O,D是BC边上一点,BD=2,以D为圆心,DB为半径的⊙D与⊙O的位置关系为外切.
如图,等边三角形ABC的边长为10,以AC为直径作⊙O,D是BC边上一点,BD=2,以D为圆心,DB为半径的⊙D与⊙O的位置关系为外切.