题目内容
12.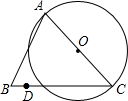 如图,等边三角形ABC的边长为10,以AC为直径作⊙O,D是BC边上一点,BD=2,以D为圆心,DB为半径的⊙D与⊙O的位置关系为外切.
如图,等边三角形ABC的边长为10,以AC为直径作⊙O,D是BC边上一点,BD=2,以D为圆心,DB为半径的⊙D与⊙O的位置关系为外切.
分析 要判断两圆的位置关系,需要明确两圆的半径和两圆的圆心距,再根据数量关系进一步判断两圆的位置关系.
两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.
解答 解:根据题意,得:圆O的直径是10,点B到点O的距离是5$\sqrt{3}$,
则5$\sqrt{3}$>5+2,
所以⊙B与⊙O的位置关系为外离.
故答案为:外切.
点评 本题考查了由数量关系来判断两圆位置关系的方法.解题的关键是了解点B到点O的距离,难度不大.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
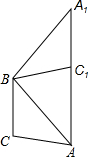 如图,△ACB中,∠BAC=40°,将△ACB绕点B逆时针旋转到△A1C1B,其中点A旋转到点A1,点C旋转到点C1,并且点A、C1、A1三点共线.
如图,△ACB中,∠BAC=40°,将△ACB绕点B逆时针旋转到△A1C1B,其中点A旋转到点A1,点C旋转到点C1,并且点A、C1、A1三点共线. 如图,A是反比例函数y=$\frac{k}{x}$的图象上一点,过点A作AB垂直于y轴于B,若△AOB的面积为3,则k的值是6.
如图,A是反比例函数y=$\frac{k}{x}$的图象上一点,过点A作AB垂直于y轴于B,若△AOB的面积为3,则k的值是6.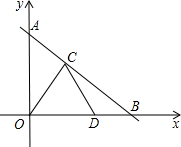 如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.
如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.