题目内容
11．
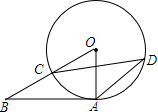如图，AB与⊙O相切于点A，BO与⊙O相交于点C，点D是优弧AC上一点，∠CDA=27°，则∠B的大小是（ ）| A． | 27° | B． | 34° | C． | 36° | D． | 54° |
分析 由切线的性质可知∠OAB=90°，由圆周角定理可知∠BOA=54°，根据直角三角形两锐角互余可知∠B=36°．
解答 解：∵AB与⊙O相切于点A，
∴OA⊥BA．
∴∠OAB=90°．
∵∠CDA=27°，
∴∠BOA=54°．
∴∠B=90°-54°=36°．
故选：C．
点评 本题主要考查的是切线的性质和圆周角定理，利用切线的性质和圆周角定理求得∠OAB=90°、∠BOA=54°是解题的关键．
练习册系列答案
相关题目
1．下面性质中菱形具有而平行四边形没有的性质是（ ）
| A． | 对角相等 | B． | 对角线互相平分 | C． | 对角线互相垂直 | D． | 对边平行 |
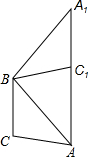如图，△ACB中，∠BAC=40°，将△ACB绕点B逆时针旋转到△A1C1B，其中点A旋转到点A1，点C旋转到点C1，并且点A、C1、A1三点共线．