题目内容
为了加强食品安全管理,有关部门对某超市的甲乙两种品牌食用油共抽取18瓶进行检测,检测结果分为“优秀、合格、不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图.
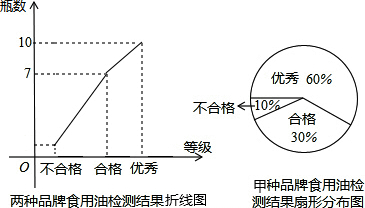
(1)抽取检测的18瓶食用油,其中不合格的有 瓶;
(2)甲种品牌被抽取了 瓶用于检测,乙种品牌被抽取了 瓶用于检测;
(3)在该超市购买一瓶乙品牌的食用油,能买到“优秀”级的概率等于 .

(1)抽取检测的18瓶食用油,其中不合格的有
(2)甲种品牌被抽取了
(3)在该超市购买一瓶乙品牌的食用油,能买到“优秀”级的概率等于
考点:折线统计图,扇形统计图,概率公式
专题:
分析:(1)根据折线统计图提供的数据,用抽取检测的总瓶数18减去“优秀”、“合格”两个等级的瓶数,所得的差即为“不合格”的瓶数;
(2)由(1)可知,“不合格”等级的有1瓶,读扇形统计图可知甲种品牌有“不合格”等级,且只有1瓶,由此可求出甲种品牌的数量,据此解答即可;
(3)根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数;二者的比值就是其发生的概率的大小.
(2)由(1)可知,“不合格”等级的有1瓶,读扇形统计图可知甲种品牌有“不合格”等级,且只有1瓶,由此可求出甲种品牌的数量,据此解答即可;
(3)根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数;二者的比值就是其发生的概率的大小.
解答:解:(1)由图可知,抽取检测的18瓶食用油,其中优秀的有10瓶,合格的有7瓶,
所以不合格的有:18-10-7=1(瓶);
(2)1÷10%=10(瓶),18-10=8(瓶),
即甲种品牌有10瓶,乙种品牌有8瓶.
(3)∵甲,乙优秀瓶总数为10瓶,其中甲品牌食用油的优秀占到60%,
∴甲的优秀瓶数为10×60%=6(瓶),
∴乙的优秀瓶数为:10-6=4(瓶),
又∵乙种品牌共有8瓶,
∴能买到“优秀”等级的概率是
=
.
故答案为1;10,8;
.
所以不合格的有:18-10-7=1(瓶);
(2)1÷10%=10(瓶),18-10=8(瓶),
即甲种品牌有10瓶,乙种品牌有8瓶.
(3)∵甲,乙优秀瓶总数为10瓶,其中甲品牌食用油的优秀占到60%,
∴甲的优秀瓶数为10×60%=6(瓶),
∴乙的优秀瓶数为:10-6=4(瓶),
又∵乙种品牌共有8瓶,
∴能买到“优秀”等级的概率是
| 4 |
| 8 |
| 1 |
| 2 |
故答案为1;10,8;
| 1 |
| 2 |
点评:本题考查的是折线统计图与扇形统计图的运用及概率公式.读懂统计图,从统计图中得到必要的信息是解决问题的关键.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.扇形图可以清楚地看出各部分数量和总数量之间的关系.概率=所求情况数与总情况数之比.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
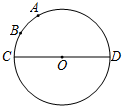 如图,已知⊙O的直径CD的长为2,
如图,已知⊙O的直径CD的长为2,
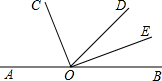 如果,O是直线AB上的一点,射线OC、OE分别平分∠AOD和∠BOD.
如果,O是直线AB上的一点,射线OC、OE分别平分∠AOD和∠BOD. 如图,已知△ABC中,AB=AC,∠A=36°.
如图,已知△ABC中,AB=AC,∠A=36°.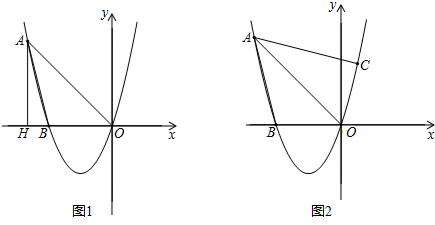
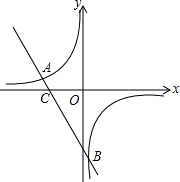 如图所示,直线y=-2x+b与反比例函数y=
如图所示,直线y=-2x+b与反比例函数y= 如图,已知双曲线y=
如图,已知双曲线y=