题目内容
已知点A(0,-4),B(8,0)和C(a,a),若过点C的圆的圆心是线段AB的中点,则这个圆的半径的最小值等于 .
考点:一次函数综合题
专题:
分析:首先求得AB的中点D的坐标,然后求得经过点D且垂直于直线y=x的直线的解析式,然后求得与y=x的交点坐标,再求得交点与D之间的距离即可.
解答:解:理解过圆心C的直线与一次函数y=x垂直的交点即为这个圆的半径的最小值.
AB的中点D的坐标是:(4,-2).
∵C(a,a)在一次函数y=x上,
∴设过D且与直线y=x垂直的直线的解析式是y=-x+b,
把(4,-2)代入解析式得:-4+b=-2,
解得:b=2,
则函数解析式是y=-x+2.
根据题意得:
,
解得:
,
则交点的坐标是(1,1).
则这个圆的半径的最小值是:
=3
.
故答案是:3
.
AB的中点D的坐标是:(4,-2).
∵C(a,a)在一次函数y=x上,
∴设过D且与直线y=x垂直的直线的解析式是y=-x+b,
把(4,-2)代入解析式得:-4+b=-2,
解得:b=2,
则函数解析式是y=-x+2.
根据题意得:
|
解得:
|
则交点的坐标是(1,1).
则这个圆的半径的最小值是:
| (4-1)2+(-2-1)2 |
| 2 |
故答案是:3
| 2 |
点评:此题考查一次函数的综合运用,两点之间的距离公式,以及两直线垂直的条件,正确理解C(a,a),一定在直线y=x上是关键.

练习册系列答案
相关题目
点P(-3,5)到y轴的距离是( )
| A、3 | B、-3 | C、5 | D、-5 |
 如图,已知双曲线y=
如图,已知双曲线y= 如图,点A的坐标为(-1,0),点B的坐标为(4,0),以AB为直径⊙O,交y轴的负半轴于点C.若二次函数y=ax2+bx+c的图象经过A,C,B.已知点P是该抛物线上的动点,当∠APB是直角时,则满足要求的点P坐标为
如图,点A的坐标为(-1,0),点B的坐标为(4,0),以AB为直径⊙O,交y轴的负半轴于点C.若二次函数y=ax2+bx+c的图象经过A,C,B.已知点P是该抛物线上的动点,当∠APB是直角时,则满足要求的点P坐标为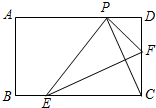 如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为
如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为