题目内容
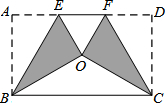 将矩形纸片ABCD按如图方式折叠,折痕是BE、CF,折叠后点A和点D重合在点O处,形成的△EOF是等边三角形,当
将矩形纸片ABCD按如图方式折叠,折痕是BE、CF,折叠后点A和点D重合在点O处,形成的△EOF是等边三角形,当| AB |
| AD |
| 1 |
| n |
考点:翻折变换(折叠问题)
专题:
分析:由△EOF是等边三角形,可得EF=OE=OF,∠OEF=60°,又由由折叠的性质可得:OE=AE,OF=BF,∠AEB=∠OEB,则可得AD=3AE,∠AEB=60°,则可证得AB=
AE,继而求得答案.
| 3 |
解答:解:∵△EOF是等边三角形,
∴EF=OE=OF,∠OEF=60°,
由折叠的性质可得:OE=AE,OF=BF,∠AEB=∠OEB,
∴AD=3AE,∠AEB=
=60°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴tan∠AEB=
=
,
∴AB=
AE,
∴
=
=
=
,
∴n=
.
故答案为:
.
∴EF=OE=OF,∠OEF=60°,
由折叠的性质可得:OE=AE,OF=BF,∠AEB=∠OEB,
∴AD=3AE,∠AEB=
| 180°-∠OEF |
| 2 |
∵四边形ABCD是矩形,
∴∠A=90°,
∴tan∠AEB=
| AB |
| AE |
| 3 |
∴AB=
| 3 |
∴
| AB |
| AD |
| ||
| 3AE |
| 1 | ||
|
| 1 |
| n |
∴n=
| 3 |
故答案为:
| 3 |
点评:此题考查了折叠的性质、等边三角形的性质、矩形的性质以及三角函数等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,已知△ABC中,AB=AC,∠A=36°.
如图,已知△ABC中,AB=AC,∠A=36°.
 如图所示,直线y=-2x+b与反比例函数y=
如图所示,直线y=-2x+b与反比例函数y= 如图,已知双曲线y=
如图,已知双曲线y= 如图,点A的坐标为(-1,0),点B的坐标为(4,0),以AB为直径⊙O,交y轴的负半轴于点C.若二次函数y=ax2+bx+c的图象经过A,C,B.已知点P是该抛物线上的动点,当∠APB是直角时,则满足要求的点P坐标为
如图,点A的坐标为(-1,0),点B的坐标为(4,0),以AB为直径⊙O,交y轴的负半轴于点C.若二次函数y=ax2+bx+c的图象经过A,C,B.已知点P是该抛物线上的动点,当∠APB是直角时,则满足要求的点P坐标为