题目内容
5．已知多项式x2+2y2-4x+4y+10，其中x，y为任意实数，那么当x，y分别取何值时，多项式的值达到最小值，最小值为（ ）| A． | 2 | B． | $\frac{5}{2}$ | C． | 4 | D． | 10 |
分析 代数式配方变形后，利用非负数的性质求出最小值．
解答 解：∵（x-2）2≥0，（y+1）2≥0，
∴式x2+2y2-4x+4y+10=（x-2）2+2（y+1）2+4≥4，
则当x=-2，y=-1时，代数式取得最小值4．
故选：C．
点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．已知在正比例函数y=-2x的图象上，有三点（-3，y1）、（-1，y2）、（2，y3），则y1，y2，y3的大小关系为（ ）
| A． | y2＞y1＞y3 | B． | y1＞y3＞y2 | C． | y1＞y2＞y3 | D． | 无法确定 |
13．
如图一场暴雨后，垂直于地面的一棵树在距地面5米的C处折断，树尖B恰好碰到地面，经测量AB=12米，则原树高为（ ）
如图一场暴雨后，垂直于地面的一棵树在距地面5米的C处折断，树尖B恰好碰到地面，经测量AB=12米，则原树高为（ ）| A． | 22米 | B． | 18米 | C． | 17米 | D． | 13米 |
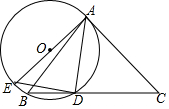如图，△ABC中，AB=AC，点D为BC上一点，过A，B，D三点作⊙O，AE是⊙O的直径，AC是⊙O的切线交BD的延长线于点C，连接DE．
17．当x=1时，代数式ax3+bx+2的值是1，当x=-1时，代数式ax3+bx-2的值是（ ）
| A． | -2 | B． | -1 | C． | 0 | D． | 1 |
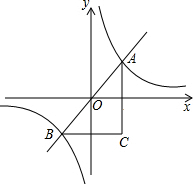如图，反比例函数y=$\frac{2}{x}$的图象与直线y=kx（k＞0）相交于A、B两点，AC∥y轴，BC∥x轴，则△ABC的面积等于4个面积单位．