题目内容
20.已知x=$\frac{1}{\sqrt{3}-\sqrt{2}}$,求$\sqrt{(x-\frac{1}{x})^{2}+4}$-$\sqrt{(x+\frac{1}{x})^{2}-4}$的值.分析 先利用完全平方公式和二次根式的性质得到原式=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|,再利用分母有理化得到x=$\sqrt{3}$+$\sqrt{2}$,且$\frac{1}{x}$=$\sqrt{3}$-$\sqrt{2}$,然后利用绝对值的意义计算原式的值.
解答 解:原式=$\sqrt{(x+\frac{1}{x})^{2}}$-$\sqrt{(x-\frac{1}{x})^{2}}$
=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|,
∵x=$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$,
∴$\frac{1}{x}$=$\sqrt{3}$-$\sqrt{2}$,
∴原式=|$\sqrt{3}$+$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$|-|$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$|
=2$\sqrt{3}$-2$\sqrt{2}$.
点评 本题考查了分母有理化:分母有理化是指把分母中的根号化去.分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知x=255,y=344,z=433,则x,y,z的大小关系为( )
| A. | x<z<y | B. | x<y<z | C. | y<z<x | D. | z<y<x |
5.已知多项式x2+2y2-4x+4y+10,其中x,y为任意实数,那么当x,y分别取何值时,多项式的值达到最小值,最小值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 4 | D. | 10 |
12.不等式组$\left\{\begin{array}{l}{x+2>1}\\{3-x≥0}\end{array}\right.$的解是( )
| A. | x<-1 | B. | x≥3 | C. | -1<x≤3 | D. | 无解 |
10.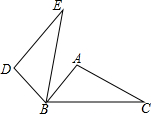 如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
 如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )| A. | 50° | B. | 70° | C. | 80° | D. | 90° |
 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.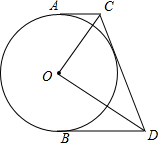 如图,已知AC,BD与⊙O相切于点A,B,且AC∥BD,若∠COD=90°,求证:CD是⊙O的切线.
如图,已知AC,BD与⊙O相切于点A,B,且AC∥BD,若∠COD=90°,求证:CD是⊙O的切线.