题目内容
13.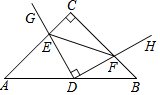 在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③S四边形CEDF=$\frac{1}{2}$S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )
在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③S四边形CEDF=$\frac{1}{2}$S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
分析 连接CD根据等腰直角三角形的性质就可以得出△ADE≌△CDF,就可以得出AE=CF,进而得出CE=BF,就有AE+BF=AC,由勾股定理就可以求出结论.
解答 解:连接CD,∵AC=BC,点D为AB中点,∠ACB=90°,
∴AD=CD=BD=$\frac{1}{2}$AB.∠A=∠B=∠ACD=∠BCD=45°,∠ADC=∠BDC=90°.
∴∠ADE+∠EDC=90°,
∵∠EDC+∠FDC=∠GDH=90°,
∴∠ADE=CDF.
在△ADE和△CDF中,$\left\{\begin{array}{l}{∠A=∠DCB}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$,
∴△ADE≌△CDF(ASA),
∴AE=CF,DE=DF,S△ADE=S△CDF.
∵AC=BC,
∴AC-AE=BC-CF,
∴CE=BF.
∵AC=AE+CE,
∴AC=AE+BF.
∵AC2+BC2=AB2,
∴AC=$\frac{\sqrt{2}}{2}$AB,
∴AE+BF=$\frac{\sqrt{2}}{2}$AB.
∵DE=DF,∠GDH=90°,
∴△DEF始终为等腰直角三角形.
∵CE2+CF2=EF2,
∴AE2+BF2=EF2.
∵S四边形CEDF=S△EDC+S△EDF,
∴S四边形CEDF=S△EDC+S△ADE=$\frac{1}{2}$S△ABC.
∴正确的有①②③④.
故选D.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,三角形的面积公式的运用,解答时证明△ADE≌△CDF是关键.

练习册系列答案
相关题目
3.如果关于x的一元二次方程mx2+x+m=0有两个实数根,那么( )
| A. | 两根互为相反数 | B. | 两根相等 | C. | 两根互为倒数 | D. | 两根和为1 |
1.关于x的不等式组$\left\{\begin{array}{l}3x-1>4({x-1})\\ x<a\end{array}\right.$的解集为x<3,那么a的取值范围为( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
8.将抛物线y=2x2先向右平移4个单位,再向上平移5个单位,得到的新抛物线的解析式为( )
| A. | y=2(x+4)2+5 | B. | y=2(x-4)2+5 | C. | y=2(x+4)2-5 | D. | y=2(x-4)2-5 |
2.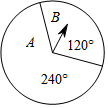 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )
 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
3.已知∠α是锐角,∠β是钝角,且∠α+∠β=180°,那么下列结论正确的是( )
| A. | ∠α的补角和∠β的补角相等 | B. | ∠α的余角和∠β的补角相等 | ||
| C. | ∠α的余角和∠β的补角互余 | D. | ∠α的余角和∠β的补角互补 |
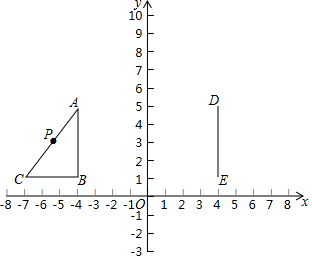 如图,在平面直角坐标系中,Rt△ABC的顶点A(-4,5),B(-4,1),∠B=90°,AC=5,点P是AC的中点,线段DE的两个端点坐标分别为D(4,5),E(4,1).
如图,在平面直角坐标系中,Rt△ABC的顶点A(-4,5),B(-4,1),∠B=90°,AC=5,点P是AC的中点,线段DE的两个端点坐标分别为D(4,5),E(4,1).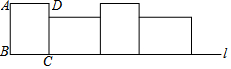 如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿直线l右翻动(不滑动)至如图位置
如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿直线l右翻动(不滑动)至如图位置