题目内容
15．已知x+$\frac{1}{x}$=$\frac{5}{2}$，求代数式x3+$\frac{1}{{x}^{3}}$的值．分析 把已知等式两边平方求出x2+$\frac{1}{{x}^{2}}$的值，原式利用立方和公式变形，将各自的值代入计算即可求出值．
解答 解：把x+$\frac{1}{x}$=$\frac{5}{2}$，两边平方得：（x+$\frac{1}{x}$）2=x2+2+$\frac{1}{{x}^{2}}$=$\frac{25}{4}$，即x2+$\frac{1}{{x}^{2}}$=$\frac{17}{4}$，
则原式=（x+$\frac{1}{x}$）（x2-1+$\frac{1}{{x}^{2}}$）=$\frac{5}{2}$×$\frac{13}{4}$=$\frac{65}{8}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
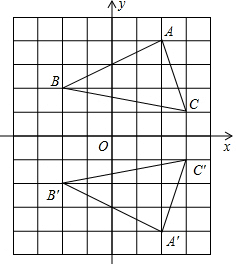（1）如图所示，写出直角坐标系中△ABC与△A′B′C′各点的坐标，并判断这两个三角形是通过怎样的变化得到的；
如图，A、B、C三点在数轴上，点C在点A与点B之间，且AC：BC=1：5