题目内容
5.能使平行四边形ABCD为正方形的条件是AC=BD且AC⊥BD或AB=BC且AB⊥BC等.(填一个即可)分析 本题是开放题,可以针对正方形的判定方法,由给出条件四边形ABCD为平行四边形,加上条件AC=BD根据对角线相等的平行四边形为矩形,得到ABCD为矩形,再加上对角线AC与BD垂直,根据对角线垂直的矩形是正方形即可得证;或加上邻边AB与BC相等,根据邻边相等的平行四边形是菱形,得到ABCD为菱形,再加上AB垂直BC,即有一个角是直角的菱形为正方形,即可得证.
解答 解:如图所示: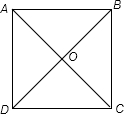 添加的条件是AC=BD且AC⊥BD,或AB=BC且AB⊥BC,平行四边形ABCD为正方形;理由如下:
添加的条件是AC=BD且AC⊥BD,或AB=BC且AB⊥BC,平行四边形ABCD为正方形;理由如下:
添加的条件时AC=BD且AC⊥BD时;
∵四边形ABCD是平行四边形.又AC=BD,
∴四边形ABCD是矩形,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴四边形ABCD是正方形;
添加的条件是AB=BC且AB⊥BC时;
∵四边形ABCD是平行四边形.AB=BC,
∴四边形ABCD是菱形,
又∵AB⊥BC,即∠ABC=90°,
∴四边形ABCD是矩形,
∴四边形ABCD是正方形;
故答案为:AC=BD且AC⊥BD或AB=BC且AB⊥BC.
点评 本题是一道开放型题目,主要考查矩形、菱形及正方形的判定;熟练掌握矩形、菱形、正方形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
