Question

6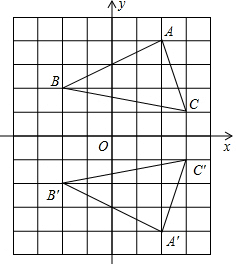．（1）如图所示，写出直角坐标系中△ABC与△A′B′C′各点的坐标，并判断这两个三角形是通过怎样的变化得到的；
（2）如果点M（m+1，n-3）与点M′（2m+1，-8+n）是两个三角中的对应点，求m，n的值．

Answer 1

分析 （1）根据各点在坐标系中的位置写出各点坐标，再由两三角形各点坐标的关系即可得出结论；
（2）根据（1）中两三角形对应点坐标的关系即可得出结论．

解答 解：（1）由图可知A（2，4），B（-2，2），C（3，1），A′（2，-4），B′（-2，-2），C′（3，-1），
∵各对应点的横坐标不变，纵坐标互为相反数，
∴△ABC与△A′B′C′关于x轴对称；

（2）∵由（1）知，△ABC与△A′B′C′关于x轴对称，、
∴$\left\{\begin{array}{l}m+1=2m+1\\ n-3=8-n\end{array}\right.$，
解得$\left\{\begin{array}{l}m=0\\ n=\frac{11}{2}\end{array}\right.$．

点评 本题考查的是作图-轴对称变换，熟知关于x轴对称的点的坐标特点是解答此题的关键．