题目内容
11．一个圆锥的侧面展开图是半径为8，圆心角为120°的扇形，则这个圆锥的高为（ ）| A． | $\frac{16}{3}\sqrt{2}$cm | B． | $\frac{16}{3}$cm | C． | $\frac{8}{3}\sqrt{2}$cm | D． | $\frac{8}{3}$cm |
分析 设圆锥的底面圆的半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2π•r=$\frac{120•π•8}{180}$，然后求出r后利用勾股定理计算圆锥的高．
解答 解：设圆锥的底面圆的半径为r，
根据题意得2π•r=$\frac{120•π•8}{180}$，解得r=$\frac{8}{3}$，
所以圆锥的高=$\sqrt{{8}^{2}-（\frac{8}{3}）^{2}}$=$\frac{16\sqrt{2}}{3}$．
故选A．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
阅读快车系列答案
相关题目
1．
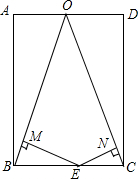如图，在矩形ABCD中，AB=3，BC=2，O是AD的中点，连接OB、OC，点E在线段BC上（点E不与点B、C重合），过点E作EM⊥OB于M，EN⊥OC于N，则EM+EN的值为（ ）
如图，在矩形ABCD中，AB=3，BC=2，O是AD的中点，连接OB、OC，点E在线段BC上（点E不与点B、C重合），过点E作EM⊥OB于M，EN⊥OC于N，则EM+EN的值为（ ）| A． | 6 | B． | 1.5 | C． | $\frac{3}{10}\sqrt{10}$ | D． | $\frac{3}{5}\sqrt{10}$ |
19．已知一个正多边形的每个外角都等于72°，则这个正多边形是（ ）
| A． | 正五边形 | B． | 正六边形 | C． | 正七边形 | D． | 正八边形 |
3．已知关于x的不等式ax＞b的解为x＜3，那么下列关于x的不等式中解为x＞3的是（ ）
| A． | -2ax＞-2b | B． | 2ax＞2b | C． | ax+2＞b+2 | D． | ax-2＞b-2 |
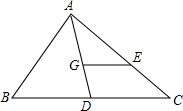如图，点G是△ABC的重心，GE∥BC，如果BC=12，那么线段GE的长为4．