题目内容
18．矩形ABCD中，AB=4，BC=$\sqrt{3}$，点E在AB上，EF∥BC，交CD于F，且矩形AEFD∽矩形EFCB，则AE等于（ ）| A． | $\frac{3}{4}$ | B． | 1或2 | C． | 1或3 | D． | 2或3 |
分析 根据相似多边形的对应边成比例列出比例式，计算即可．
解答 解：∵矩形AEFD∽矩形EFCB，
∴$\frac{AE}{EF}$=$\frac{EF}{FC}$，即$\frac{AE}{\sqrt{3}}$=$\frac{\sqrt{3}}{4-AE}$，
解得，AE=1或3，
故选：C．
点评 本题考查的是相似多边形的性质，掌握相似多边形的对应边成比例是解题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
已知∠α，求作∠AOB使∠AOB=∠α．
如图所示，已知∠1=∠2，∠B=60°，∠ACB=80°，求∠BCD的度数．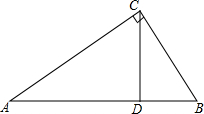
如图，△ABC中，∠ACB=90°，AB=$\sqrt{8}$，BC=$\sqrt{2}$．
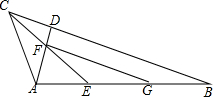如图，△ABC为直角三角形，∠BAC=90°，AD⊥BC于D，∠ACB的平分线交AD于点F，交AB于点E，FG∥BC交AB于G，AE=3，AB=8，求EG的长．