题目内容
10.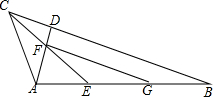 如图,△ABC为直角三角形,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于点F,交AB于点E,FG∥BC交AB于G,AE=3,AB=8,求EG的长.
如图,△ABC为直角三角形,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于点F,交AB于点E,FG∥BC交AB于G,AE=3,AB=8,求EG的长.
分析 根据角平分线的性质和三角形的面积公式得到$\frac{AC}{BC}=\frac{AE}{BE}$,同理$\frac{AF}{FD}=\frac{AC}{CD}$,代入数据求得$\frac{AE}{BE}$=$\frac{3}{5}$,$\frac{AC}{BC}=\frac{3}{5}$,设AC=3m.BC=5m,通过Rt△ACD∽△Rt△BCA,得到比例式$\frac{AC}{BC}=\frac{CD}{CA}$,然后根据平行线分线段成比例得到$\frac{AG}{AB}=\frac{AF}{AD}$,于是得到AG=5,即可得到结论.
解答 解:∵CE平分∠ACB,
∴点E到AC,BC的距离相等(用h表示)
∴$\frac{{S}_{△ACE}}{{S}_{△BCE}}$=$\frac{\frac{1}{2}AC•h}{\frac{1}{2}BC•h}$=$\frac{AC}{BC}$,
∵$\frac{{S}_{△ACE}}{{S}_{△BCE}}$=$\frac{\frac{1}{2}AE•AC}{\frac{1}{2}BE•AC}$=$\frac{AE}{BE}$,
∴$\frac{AC}{BC}=\frac{AE}{BE}$,同理$\frac{AF}{FD}=\frac{AC}{CD}$,
∵AE=3,AB=8,
∴$\frac{AE}{BE}$=$\frac{3}{5}$,
∴$\frac{AC}{BC}=\frac{3}{5}$,
设AC=3m.BC=5m,
∵∠BAC=90°,AD⊥BC,
∴Rt△ACD∽△Rt△BCA,
∴$\frac{AC}{BC}=\frac{CD}{CA}$,
∴CD=$\frac{9}{5}$m,
∴$\frac{AF}{FD}=\frac{3m}{\frac{9}{5}m}$=$\frac{5}{3}$,
∴$\frac{AF}{AD}=\frac{5}{8}$,
∵FG∥BC,
∴$\frac{AG}{AB}=\frac{AF}{AD}$,
∴AG=5,
∴EG=AG-AE=2.
点评 本题考查了平行线分线段成比例,相似三角形的判定和性质,三角形的面积,熟练掌握平行线分线段成比例定理是解题的关键.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | 成正比例 | B. | 成反比例 | ||
| C. | 有可能成正比例有可能成反比例 | D. | 无法确定 |
| A. | $\frac{3}{4}$ | B. | 1或2 | C. | 1或3 | D. | 2或3 |
 如图,在△ABC中,如果DE∥BC,DF∥AC,则不正确的是( )
如图,在△ABC中,如果DE∥BC,DF∥AC,则不正确的是( )| A. | $\frac{AE}{EC}$=$\frac{CF}{FB}$ | B. | $\frac{BF}{BC}$=$\frac{DF}{AC}$ | C. | $\frac{AC}{AE}$=$\frac{AB}{AC}$ | D. | $\frac{AD}{FC}$=$\frac{AB}{BC}$ |
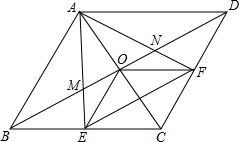 如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=60°,点E,F分别是BC,CD的中点,BD分别与AE,AF相交于点M,N,连接OE,OF,下列结论:(1)△AEF是等边三角形;(2)四边形CEOF是菱形;(3)OF⊥AE;(4)BM=MN=ND.其中正确的结论有( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=60°,点E,F分别是BC,CD的中点,BD分别与AE,AF相交于点M,N,连接OE,OF,下列结论:(1)△AEF是等边三角形;(2)四边形CEOF是菱形;(3)OF⊥AE;(4)BM=MN=ND.其中正确的结论有( )