题目内容
7．有下列说法：①两个无理数的和还是无理数；②无理数与有理数的积是无理数；③有理数与有理数的和不可能是无理数；④无限小数是无理数；③不是有限小数的不是有理数，其中正确的有（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
分析 根据无理数是无限不循环小数，可得答案．
解答 解：①两个无理数的和可能是无理数、可能是有理数，故①错误；
②无理数与有理数的积可能是无理数、可能是有理数，故②错误；
③有理数与有理数的和不可能是无理数，故③正确；
④无限不循环小数是无理数，故④错误；
⑤有限小数或无限循环小数是有理数，故⑤错误，
故选：B．
点评 本题考查了实数，无限不循环小数是无理数，有限小数或无限循环小数是有理数．
练习册系列答案
相关题目
如图，已知P是∠M0N的平分线上一点，PA⊥ON于点A，PB⊥OM于点B，你能得出的结论是AP=BP，OP垂直平分线AB（至少写两条）．
18．矩形ABCD中，AB=4，BC=$\sqrt{3}$，点E在AB上，EF∥BC，交CD于F，且矩形AEFD∽矩形EFCB，则AE等于（ ）
| A． | $\frac{3}{4}$ | B． | 1或2 | C． | 1或3 | D． | 2或3 |
15．
如图，在△ABC中，如果DE∥BC，DF∥AC，则不正确的是（ ）
如图，在△ABC中，如果DE∥BC，DF∥AC，则不正确的是（ ）| A． | $\frac{AE}{EC}$=$\frac{CF}{FB}$ | B． | $\frac{BF}{BC}$=$\frac{DF}{AC}$ | C． | $\frac{AC}{AE}$=$\frac{AB}{AC}$ | D． | $\frac{AD}{FC}$=$\frac{AB}{BC}$ |
2．
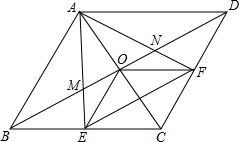如图，在菱形ABCD中，对角线AC与BD相交于点O，∠ABC=60°，点E，F分别是BC，CD的中点，BD分别与AE，AF相交于点M，N，连接OE，OF，下列结论：（1）△AEF是等边三角形；（2）四边形CEOF是菱形；（3）OF⊥AE；（4）BM=MN=ND．其中正确的结论有（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，∠ABC=60°，点E，F分别是BC，CD的中点，BD分别与AE，AF相交于点M，N，连接OE，OF，下列结论：（1）△AEF是等边三角形；（2）四边形CEOF是菱形；（3）OF⊥AE；（4）BM=MN=ND．其中正确的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．有两个一元二次方程M：ax2+bx+c=0，N：cx2+bx+a=0，其中a×c≠0，a≠c；以下列四个结论中错误的是（ ）
| A． | 如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 | |
| B． | 如果方程M有两根符号相同，那么方程N的两根符号也相同 | |
| C． | 如果5是方程M的一个根，那么$\frac{1}{5}$是方程N的一个根 | |
| D． | 如果方程M和方程N有一个相同的根，那么这个根必是x=1 |