题目内容
10.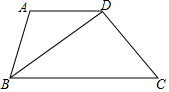 如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,则tan∠DBC=$\frac{3}{4}$.
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,则tan∠DBC=$\frac{3}{4}$.
分析 设CD=x,则BD=x+2,证出AB=AD=5,得出BE=$\frac{1}{2}$BD=$\frac{1}{2}$x+1,证明△ABE∽△CBD,得出比例式求出BC=10,由勾股定理求出CD,得出BD,再由三角函数定义即可得出结果.
解答 解:作AE⊥BD于E,如图所示: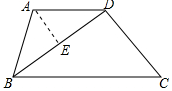
则∠AEB=90°,
设CD=x,则BD=x+2,
∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD=5,
∴BE=$\frac{1}{2}$BD=$\frac{1}{2}$x+1,
∵CD⊥BD,
∴∠BDC=90°=∠BEA,
又∵∠ABD=∠CBD,
∴△ABE∽△CBD,
∴$\frac{BE}{AB}=\frac{BD}{BC}$,即$\frac{\frac{1}{2}x+1}{5}=\frac{x+2}{bc}$,
解得:BC=10,
在Rt△BCD中,CD2+BD2=BC2,
即x2+(x+2)2=102,
解得:x=6,
∴CD=6,BD=8,
∴tan∠DBC=$\frac{6}{8}$=$\frac{3}{4}$
故答案为:$\frac{3}{4}$.
点评 本题考查了梯形的性质、等腰三角形的判定、相似三角形的判定与性质、勾股定理以及三角函数;证明三角形相似求出BC是解决问题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
20.定义一种运算:ak=ak-1+1-5([$\frac{k-1}{5}$]-[$\frac{k-2}{5}$]),其中k是正整数,且k?2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若a1=1,则a2016的值为( )
| A. | 2017 | B. | 1 | C. | 2016 | D. | 2 |
5.下列关于$\sqrt{20}$的说法中,错误的是( )
| A. | $\sqrt{20}$是无理数 | B. | 4<$\sqrt{20}$<5 | ||
| C. | $\sqrt{20}$是20的算术平方根 | D. | $\sqrt{20}$不能再化简 |
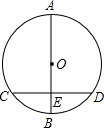 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.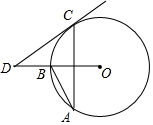 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D=30°.
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D=30°.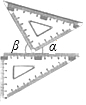 数学课上,小丽把一副三角板按如图所示的位置摆放(其中一个三角板的直角顶点在另一个三角板的直角边上),如果∠α=28°,那么∠β=62°.
数学课上,小丽把一副三角板按如图所示的位置摆放(其中一个三角板的直角顶点在另一个三角板的直角边上),如果∠α=28°,那么∠β=62°.