题目内容
1.一组按规律排列的式子:$\frac{{b}^{2}}{a}$,$-\frac{{b}^{5}}{{a}^{2}}$,$\frac{{b}^{8}}{{a}^{3}}$,$-\frac{{b}^{11}}{{a}^{4}}$,…(ab≠0),则第n的个式子是$\frac{(-1)^{n+1}{b}^{3n-1}}{{a}^{n}}$.分析 根据观察可发现规律:$\frac{(-1)^{n+1}{b}^{3n-1}}{{a}^{n}}$.
解答 解:由$\frac{{b}^{2}}{a}$,$-\frac{{b}^{5}}{{a}^{2}}$,$\frac{{b}^{8}}{{a}^{3}}$,$-\frac{{b}^{11}}{{a}^{4}}$,…(ab≠0),得
系数是(-1)n+1,b的次数是(3n-1),a的次数是n,
则第n的个式子是$\frac{(-1)^{n+1}{b}^{3n-1}}{{a}^{n}}$,
故答案为:$\frac{(-1)^{n+1}{b}^{3n-1}}{{a}^{n}}$.
点评 本题考查了分式的定义,发现规律第n个分式$\frac{(-1)^{n+1}{b}^{3n-1}}{{a}^{n}}$是解题关键.

练习册系列答案
相关题目
16. 如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
 如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
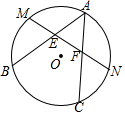 如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形.
如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形. 已知:如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.求证:DC=CF.
已知:如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.求证:DC=CF.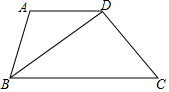 如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,则tan∠DBC=$\frac{3}{4}$.
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,则tan∠DBC=$\frac{3}{4}$.