Question

如图，一艘货轮以36km的速度在海面上航行，当它行驶到A处时，发现它的东北方向有一灯塔B，货轮继续向北航行40min后到达C点，发现灯塔B在塔北偏东75°方向，求此时货轮与灯塔B的距离（结果精确到0.01海里）．

Answer 1

考点：解直角三角形的应用-方向角问题

专题：

分析：根据题意求出AC的长，再利用锐角三角函数关系得出DC的长，即可得出BC的长．

解答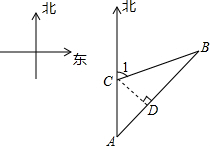：解：如图所示：过点C作CD⊥AB于点D，
∵一艘货轮以36km的速度在海面上航行，向北航行40min后到达C点，
∴AC=36×

40

60

=24（km），
∵∠A=45°，∠1=75°，
∴∠ACD=45°，∠DCB=60°，
则∠B=30°，
则DC=ACsin45°=24×

2

2

=12

2

（km），
故BC=2CD=24

2

≈33.94（km）．
答：此时货轮与灯塔B的距离约为33.94km．

点评：此题主要考查了方向角问题，根据题意作出正确辅助线是解题关键．