题目内容

8．为解方程x4-5x2+4=0，我们可设x2=y，则x4=y2，原方程可化为y2-5y+4=0．解得y1=1，y2=4，当y=1时，x2=1，所以x=±1；当y=4时，x2=4，所以x=±2．故原方程的解为x1=1，x2=-1，x3=2，x4=-2．以上解题方法主要体现的数学思想是（　　）
A．数形结合B．换元与降次C．消元D．公理化

分析 根据把x4换为y2，体现了换元的数学思想，把一元四次方程x4-5x2+4=0，变为一元二次方程y2-5y+4=0，又体现了降次的数学思想．

解答 解：本题体现了两个重要的数学数学，换元和将次的数学思想，
故选B．

点评 本题考查了用换元法解一元二次方程，掌握高次方程的解法是换元和将次是解题的关键．

练习册系列答案
相关题目
18．我市计划对1000m2的区域进行绿化，由甲、乙两个工程队合作完成．已知甲队每天能完成绿化的面积是乙队的2倍；当两队分别各完成200m2的绿化时，甲队比乙队少用2天．
（1）求甲、乙两工程队每天能完成的绿化的面积；
（2）两队合作完成此项工程，若甲队参与施工n天，试用含n的代数式表示乙队施工的天数；
（3）若甲队每天施工费用是0.6万元，乙队每天为0.25万元，且要求两队施工的天数之和不超过15天，应如何安排甲、乙两队施工的天数，使施工总费用最低？并求出最低费用．
19．如果方程2xm-1-3y2m+n=1是关于x、y的二元一次方程，那么m、n的值分别为（　　）
A．1，0B．2，-3C．1，-3D．1，1
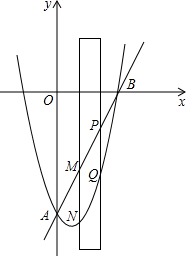16．如图，抛物线y=x2+bx+c交y轴于点A（0，-8），交x轴正半轴于点B（4，0）．
（1）抛物线的函数关系式为y=x2-2x-8；
（2）有一宽度为1的直尺平行于y轴，在点A、B之间移动，直尺两长边所在直线被线段AB和抛物线截得两线段MN（M在N上方）、PQ（P在Q上方），设M点的横坐标为m，（0＜m＜3）
①若连接MQ，求以M、P、Q为顶点的三角形和△AOB相似时，m的值；
②若连接NQ，请直接写出m为何值时，四边形MNQP的面积最大．
3．求不等式组$\left\{\begin{array}{l}{3x-2＞x+2①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$．
13．（1）计算：|-$\sqrt{2}$|+（π-3）0+（$\frac{1}{2}$）-1-2cos45°
（2）解不等式组$\left\{\begin{array}{l}{2x-1＞x+1}\\{x+8＞4x-1}\end{array}\right.$并把它的解集在数轴上表示出来．
20．（1）计算：（$\sqrt{5}$-π）0-6tan30°+（$\frac{1}{2}$）-2+|1+$\sqrt{3}$|．
（2）解不等式组$\left\{\begin{array}{l}{4（x-1）≤3（x+2）}\\{\frac{x-1}{2}＜x-4}\end{array}\right.$，并写出它的所有整数解．
17．解不等式组，并把解集用数轴表示出来．
$\left\{\begin{array}{l}{-3（x+1）-（x-3）＜8}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$．
18．分式方程$\frac{2}{x-3}=\frac{3}{x}$的解是（　　）
A．x=-9B．x=9C．x=3D．$x=\frac{9}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网