题目内容
20.(1)计算:($\sqrt{5}$-π)0-6tan30°+($\frac{1}{2}$)-2+|1+$\sqrt{3}$|.(2)解不等式组$\left\{\begin{array}{l}{4(x-1)≤3(x+2)}\\{\frac{x-1}{2}<x-4}\end{array}\right.$,并写出它的所有整数解.
分析 (1)先去掉绝对值,用零指数幂,负指数幂,三角函数,化简,最后用实数的运算即可.
(2)分别解出不等式①,②的解集确定出公共部分即可.
解答 (1)解:原式=1-6×$\frac{\sqrt{3}}{3}$+4+1+$\sqrt{3}$=4-$\sqrt{3}$.
(2)解不等式①,得x≤10.
解不等式②,得x>7.
∴原不等式组的解集为7<x≤10.
∴原不等式组的所有整数解为8,9,10.
点评 此题是实数的运算,主要考查了实数的运算,零指数幂的运算,负整数指数幂的运算,特殊三角函数值,要熟练掌握,解本题的关键是熟练掌握实数的运算顺序.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.为解方程x4-5x2+4=0,我们可设x2=y,则x4=y2,原方程可化为y2-5y+4=0.解得y1=1,y2=4,当y=1时,x2=1,所以x=±1;当y=4时,x2=4,所以x=±2.故原方程的解为x1=1,x2=-1,x3=2,x4=-2.以上解题方法主要体现的数学思想是( )
| A. | 数形结合 | B. | 换元与降次 | C. | 消元 | D. | 公理化 |
15.“慈母手中线,游子身上衣”,为了解某校1000名学生在5月8日“母亲节”期间对母亲表达感谢的方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问某校抽取学生“母亲节”期间对母亲表达感谢的方式的统计表卷调查的结果绘制成如下不完整的统计表:
(1)本次问卷调查抽取的学生共有50人,其中通过给母亲一个爱的拥抱表达感谢的学生有4人;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过帮母亲做家务表达感谢的约有多少人?
| 方式 | 频数 | 百分比 |
| 送母亲礼物 | 23 | 46% |
| 帮母亲做家务 | ||
| 给母亲一个爱的拥抱 | 8% | |
| 其他 | 15 | |
| 合计 | 100% |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过帮母亲做家务表达感谢的约有多少人?
12.不等式组$\left\{\begin{array}{l}{x-1>0}\\{2x<4}\end{array}\right.$的解是( )
| A. | x>1 | B. | x<2 | C. | 1<x<2 | D. | 无解 |
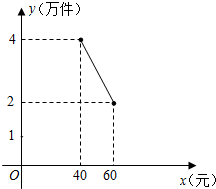 为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.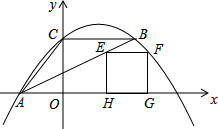 如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.
如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.