题目内容
4.先化简代数式(1+$\frac{1}{a-1}$)÷$\frac{a}{{{a^2}-2a+1}}$,然后在0≤a<4范围选取一个适当的整数作为a的值代入求值.分析 先将原式化简,然后求出该分式有意义时,a的取值范围即可求出答案.
解答 解:原式=(1+$\frac{1}{a-1}$)÷$\frac{a}{(a-1)^{2}}$
=(1+$\frac{1}{a-1}$)×$\frac{(a-1)^{2}}{a}$
=$\frac{(a-1)^{2}}{a}$+$\frac{a-1}{a}$
=$\frac{{a}^{2}-2a+1+a-1}{a}$
=$\frac{{a}^{2}-a}{a}$
=a-1
∵$\left\{\begin{array}{l}{a-1≠0}\\{a≠0}\end{array}\right.$,
∴a≠0且a≠1,
∵0≤a<4
∴a=2时,
原式=1
点评 本题考查分式的化简运算,解题的关键是将原式分式化简,本题属于基础题型.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
19.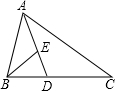 如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
 如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )| A. | 16:45 | B. | 2:9 | C. | 1:9 | D. | 1:3 |
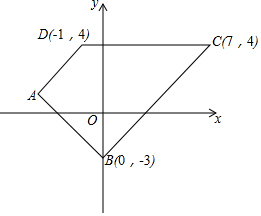 图中的A(-4,1)、B(0,-3)、C(7,4)和D(-1,4)是一个梯形的顶点.其中AD∥BC及AB⊥AD.
图中的A(-4,1)、B(0,-3)、C(7,4)和D(-1,4)是一个梯形的顶点.其中AD∥BC及AB⊥AD.