题目内容
12.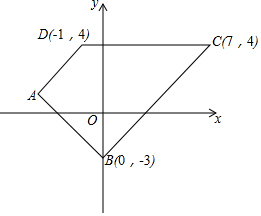 图中的A(-4,1)、B(0,-3)、C(7,4)和D(-1,4)是一个梯形的顶点.其中AD∥BC及AB⊥AD.
图中的A(-4,1)、B(0,-3)、C(7,4)和D(-1,4)是一个梯形的顶点.其中AD∥BC及AB⊥AD.(a)求AD、AB和BC的长度;
(b)求梯形ABCD的周长;
(c)求梯形ABCD的面积;
(如有需要,取答案准确至三位有效数字)
分析 (a)由两点间的距离公式即可得出AD、AB和BC的长度;
(b)求出CD=8,即可得出梯形的周长;
(c)由梯形面积公式即可得出答案.
解答 解:(a)∵A(-4,1)、B(0,-3)、C(7,4)、D(-1,4),
∴AD=$\sqrt{(-1+4)^{2}+(4-1)^{2}}$=3$\sqrt{2}$,AB=$\sqrt{(-4)^{2}+(-3-1)^{2}}$=4$\sqrt{2}$,BC=$\sqrt{({7}^{2}+(4+3)^{2}}$=7$\sqrt{2}$;
(b)∵CD=7+1=8,
∴梯形ABCD的周长=4$\sqrt{2}$+7$\sqrt{2}$+3$\sqrt{2}$+8=14$\sqrt{2}$+8;
(c)根据题意得:四边形ABCD为直角梯形,
∴梯形ABCD的面积=$\frac{1}{2}$(AD+BC)•AB=$\frac{1}{2}$(3$\sqrt{2}$+7$\sqrt{2}$)•4$\sqrt{2}$=80.
点评 本题主要考查了坐标与图形性质、两点间的距离公式以及梯形周长和面积的计算;求出AD、AB和BC的长度是解决问题的关键.

练习册系列答案
相关题目
17.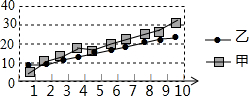 某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
 某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )| A. | 甲得分的平均数小于乙得分的平均数 | |
| B. | 甲得分的中位数小于乙得分的中位数 | |
| C. | 甲得分的方差大于乙得分的方差 | |
| D. | 甲得分的最小值大于乙得分的最小值 |
 王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示:
王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示: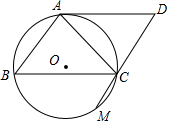 如图,AC是?ABCD的对角线,△ABC的外接圆O交DC的延长线于点M,AC=CD.
如图,AC是?ABCD的对角线,△ABC的外接圆O交DC的延长线于点M,AC=CD.