题目内容
15.在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).(1)求抛物线的表达式;
(2)求抛物线的顶点坐标及与x轴交点的坐标.
分析 (1)把两个已知点的坐标代入y=x2+bx+c得到关于b、c的方程组,然后解方程组即可确定抛物线解析式;
(2)把(1)中的一般式配成顶点式即可得到抛物线的顶点坐标,然后通过解x2-2x-3=0可得到抛物线与x轴的交点坐标.
解答 解:(1)把(0,-3),(2,-3)代入y=x2+bx+c得$\left\{\begin{array}{l}{4+2b+c=-3}\\{c=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
所以抛物线解析式为y=x2-2x-3;
(2)因为y=x2-2x-3=(x-1)2-4,
所以抛物线的顶点坐标为(1,-4);
当y=0时,x2-2x-3=0,解得x1=3,x2=-1,
所以抛物线与x轴的交点坐标为(-1,0),(3,0).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了待定系数法求二次函数解析式.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
6.下列整式运式计算的是结果为a6是( )
| A. | a3+a3 | B. | (a2)3 | C. | a12÷a2 | D. | (a2)4 |
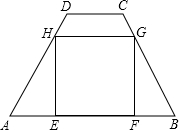 如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.
如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.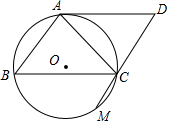 如图,AC是?ABCD的对角线,△ABC的外接圆O交DC的延长线于点M,AC=CD.
如图,AC是?ABCD的对角线,△ABC的外接圆O交DC的延长线于点M,AC=CD.