题目内容
11.若设分式$\frac{x}{x-1}$的值为y,则有y=$\frac{x}{x-1}$(1)分别求当x=2及x=$\frac{1}{2}$时,y的值;
(2)当x=a时,y=c;x=b时,y=d,若c+d=1,求证:ab=1;
(3)求代数式$\frac{1}{x}$+$\frac{1}{y}$+(1-x)(1-y)的值;
(4)设m=$\frac{{y}_{1}{+y}_{2}-2}{2}$,n=$\frac{2}{{x}_{1}{+x}_{2}-2}$,其中y1、y2分别是分式$\frac{x}{x-1}$中的x取x1、x2(x2>x1>1)时所对应的值,试判断m、n的大小,并说明理由.
分析 (1)分别把x=2和x=$\frac{1}{2}$代入y=$\frac{x}{x-1}$中求出对应y的值即可;
(2)根据题意得$\frac{a}{a-1}$+$\frac{b}{b-1}$=1,然后去分母整理即可得到结论;
(3)把y=$\frac{x}{x-1}$代入原式,然后进行分式的混合运算和得到原式的值;
(4)先化简m得m=$\frac{{x}_{1}+{x}_{2}-2}{2({x}_{1}-1)({x}_{2}-1)}$,再计算m-n得到m-n=$\frac{({x}_{1}-{x}_{2})^{2}}{2({x}_{1}-1)({x}_{2}-1)({x}_{1}+{x}_{2}-2)}$,然后利用x2>x1>1可判断m-n>0,从而得到m与n的大小.
解答 (1)解:当x=2时,y=$\frac{2}{2-1}$=2;当x=$\frac{1}{2}$时,y=$\frac{\frac{1}{2}}{\frac{1}{2}-1}$=-1;
(2)证明:因为当x=a时,y=c;x=b时,y=d,
所以c=$\frac{a}{a-1}$,d=$\frac{b}{b-1}$,
而c+d=1,
所以$\frac{a}{a-1}$+$\frac{b}{b-1}$=1,
即a(b-1)+b(a-1)=(a-1)(b-1),
ab-a+ab-b=ab-a-b+1,
所以ab=1;
(3)解:原式=$\frac{1}{x}$+$\frac{x-1}{x}$+(1-x)(1-$\frac{x}{x-1}$)
=$\frac{1+x-1}{x}$+(1-x)$\frac{x-1-x}{x-1}$
=1+1
=2;
(4)解:m=$\frac{\frac{{x}_{1}}{{x}_{1}-1}+\frac{{x}_{2}}{{x}_{2}-1}-2}{2}$=$\frac{{x}_{1}({x}_{2}-1)+{x}_{2}({x}_{1}-1)-2({x}_{1}-1)({x}_{2}-1)}{2({x}_{1}-1)({x}_{2}-1)}$=$\frac{{x}_{1}+{x}_{2}-2}{2({x}_{1}-1)({x}_{2}-1)}$,
m-n=$\frac{{x}_{1}+{x}_{2}-2}{2({x}_{1}-1)({x}_{2}-1)}$-$\frac{2}{{x}_{1}+{x}_{2}-2}$
=$\frac{({x}_{1}+{x}_{2}-2)^{2}-4({x}_{1}-1)({x}_{2}-1)}{2({x}_{1}-1)({x}_{2}-1)({x}_{1}+{x}_{2}-2)}$
=$\frac{({x}_{1}-{x}_{2})^{2}}{2({x}_{1}-1)({x}_{2}-1)({x}_{1}+{x}_{2}-2)}$,
因为x2>x1>1,
所以x1-1>0,x2-1>0,x1+x2-2>0,
而(x1-x2)2>0,
∴m-n>0,
即m>n.
点评 本题考查了分式的混合运算:先进行括号内的运算,再进行分式的乘除运算,然后进行分式的加减运算.利用求差法比较大小是解决(4)小题的关键.

| A. | 4 | B. | 12 | C. | 24 | D. | 28 |
 如图,△ABC中,∠ACB=90°,D是AB中点,过点B作直线CD的垂线,垂足为E.求证:∠EBC=∠A.
如图,△ABC中,∠ACB=90°,D是AB中点,过点B作直线CD的垂线,垂足为E.求证:∠EBC=∠A. 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF.
如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF.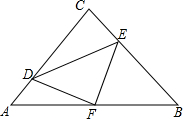 如图,Rt△ABC中,∠ACB=90°,AC=BC=8.D、E是边AC、BC边上的动点,D从A出发向C运动,同时E以相同的速度从C出发向B运动,E运动到B停止.F为AB中点.
如图,Rt△ABC中,∠ACB=90°,AC=BC=8.D、E是边AC、BC边上的动点,D从A出发向C运动,同时E以相同的速度从C出发向B运动,E运动到B停止.F为AB中点.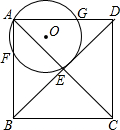 如图,在正方形ABCD中,E为对角线AC,BD的交点,经过点A和点E作⊙O,分别交AB、AD于点F、G.已知正方形边长为5,⊙O的半径为2,则AG•GD的值为9.
如图,在正方形ABCD中,E为对角线AC,BD的交点,经过点A和点E作⊙O,分别交AB、AD于点F、G.已知正方形边长为5,⊙O的半径为2,则AG•GD的值为9.