Question

3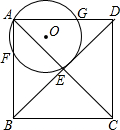．如图，在正方形ABCD中，E为对角线AC，BD的交点，经过点A和点E作⊙O，分别交AB、AD于点F、G．已知正方形边长为5，⊙O的半径为2，则AG•GD的值为9．

Answer 1

分析 连接EF、FG，GE如图，根据正方形的性质得到∠BAD=90°，∠BEA=90°证得△BPF≌△APE，根据全等三角形的性质得到BF=AE，求得DE=AF，根据圆周角定理得到GF为⊙O的直径，得到GF=4，根据勾股定理得到AF²+AG²=GF²=16，由①②联立起来组成方程组，即可得到结论．

解答 解：连接EF、FG，GE如图，
∵四边形ABCD为正方形，
∴∠BAD=90°，∠BEA=90°
∴∠FEG=90°，
∴∠BEF=∠AEG，
又∵∠FBE=∠EAG=45°，
在△BEF与△AGE中，$\left\{\begin{array}{l}{∠BEF=∠AGE}\\{∠EBF=∠EAG}\\{BE=AE}\end{array}\right.$，
∴△BPF≌△APE，
∴BF=AE，
而AB=AD，
∴DE=AF，
∵∠BAD=90°，
∴GF为⊙O的直径，
而⊙O的半径为2，
∴GF=4，
∴AF²+AG²=GF²=16①，
而DG=AF，
DG²+AG²=16；
又∵AD=AG+GD=AB，
∴AG+GD=5②，
由①②联立起来组成方程组，解得：AG=$\frac{5+\sqrt{7}}{2}$，GD=$\frac{5-\sqrt{7}}{2}$或AG=$\frac{5-\sqrt{7}}{2}$，GD=$\frac{5+\sqrt{7}}{2}$，
∴AG•GD=4.5．
故答案为：4.5．

点评 本题考查了全等三角形的判定和性质，圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．同时考查了直径所对的圆周角为直角、圆内接四边形的性质、正方形的性质以及方程组的解法．