题目内容
16.①设a>b>0,a2+b2-6ab=0,则$\frac{a+b}{a-b}$的值为$\sqrt{2}$;②若$\frac{1}{a}-\frac{1}{b}=2$,则$\frac{2a-13ab-2b}{a-2ab-b}$=$\frac{17}{4}$.
分析 ①把已知等式的-6ab变为2ab-8ab,利用加法的交换律及结合律使之能用完全平方公式,然后根据a与b都大于0,开方即可表示出a+b;把-6ab变为-2ab-4ab,同理结合后,根据a大于b,且a与b都大于0,开方即可表示出a-b,然后把所求的式子提取-1后,将表示出的a+b及a-b代入,化简即可求出值;
②先根据题意得出a-b=-2ab,再代入代数式进行计算即可.
解答 解:①∵a2+b2-6ab=0,
∴a2+2ab+b2-8ab=0,即(a+b)2=8ab.
又∵a>b>0,
∴a+b=$\sqrt{8ab}$=2$\sqrt{2ab}$;
又∵a2+b2-6ab=0,
∴a2-2ab+b2-4ab=0,即(a-b)2=4ab,
又∵a>b>0,
∴a-b=$\sqrt{4ab}$=2$\sqrt{ab}$,
∴$\frac{a+b}{a-b}$=$\frac{2\sqrt{2ab}}{2\sqrt{ab}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$;
②∵$\frac{1}{a}-\frac{1}{b}=2$,
∴a-b=-2ab,
∴$\frac{2a-13ab-2b}{a-2ab-b}$=$\frac{2(a-b)-13ab}{(a-b)-2ab}$=$\frac{-4ab-13ab}{-2ab-2ab}$=$\frac{-17ab}{-4ab}$=$\frac{17}{4}$.
故答案为:$\frac{17}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
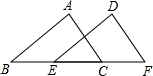 如图,在三角形ABC中,BC=8,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得的图形对应为三角形DEF,设平移的时间为t秒,当t=( )时,AD=CE.
如图,在三角形ABC中,BC=8,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得的图形对应为三角形DEF,设平移的时间为t秒,当t=( )时,AD=CE.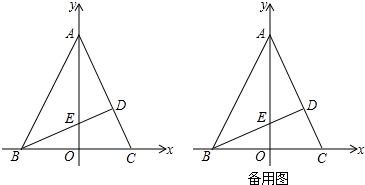
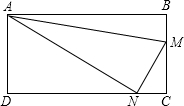 如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )
如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( ) 如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?