题目内容
19.在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A.点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2+1(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
分析 (1)由过点(0,2)且平行于x轴的直线解析式为y=2,可求出点A的坐标,由点A关于直线x=1的对称点为B,可求出点B的坐标;
(2)由抛物线C1:y=x2+bx+c经过点A,B,利用待定系数法可求出函数的解析式,将解析式配方后可得出顶点的坐标;
(3)结合图形,可得知ax2+1=2两个根的范围,从而的出结论.
解答 解:(1)过点(0,2)且平行于x轴的直线解析式为y=2,
令y=2,则有x-1=2,解得:x=3,
故A点的坐标为(3,2).
∵点A关于直线x=1的对称点为B,
∴B点的坐标为(-1,2).
(2)∵抛物线C1:y=x2+bx+c经过点A,B,
∴有$\left\{\begin{array}{l}{2=9+3b+c}\\{2=1-b+c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-2}\\{c=-1}\end{array}\right.$,
故求抛物线C1的表达式为y=x2-2x-1.
∵y=x2-2x-1=(x-1)2-2,
∴抛物线C1的顶点坐标为(1,-2).
(3)依照题意画出题形如下.
令y=2,则有ax2+1=2,解得:x=±$\frac{1}{\sqrt{a}}$,其中a>0,
∵抛物线C2:y=ax2+1(a≠0)与线段AB恰有一个公共点,
∴有$\left\{\begin{array}{l}{-\frac{1}{\sqrt{a}}<-1}\\{\frac{1}{\sqrt{a}}≤3}\end{array}\right.$,解得:$\frac{1}{9}$≤a<1.
故a的取值范围为$\frac{1}{9}$≤a<1.
点评 本题考查了待定系数法求函数解析式、二次函数的性质以及解一元一次不等式,解题的关键:(1)解一元一次方程求出点A的坐标;(2)由待定系数法找出关于b、c的二元一次方程组;(3)结合图象找出关于a的一元一次不等式组.本题属于中档题,难度不大,但涉及知识点较多,需要对二次函数足够了解才能快捷的解决问题.

 如图,在△ABC中,∠B=∠C=67.5°.
如图,在△ABC中,∠B=∠C=67.5°.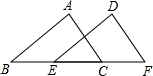 如图,在三角形ABC中,BC=8,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得的图形对应为三角形DEF,设平移的时间为t秒,当t=( )时,AD=CE.
如图,在三角形ABC中,BC=8,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得的图形对应为三角形DEF,设平移的时间为t秒,当t=( )时,AD=CE.