题目内容
6.平面直角坐标系中,点A(2,n)在第一象限,把点A向右移p个单位长度得点B.(1)写出点B的坐标;
(2)把点A向下平移4个单位长度得到点C,点C距x轴1个单位长度,若AB=AC.
①求点B的坐标;
②求三角形ABC的面积.
分析 (1)根据横坐标,右移加,左移减可得B(2+p,n);
(2)①首先根据上移加,下移减确定C(2,n-4),再根据点C距x轴1个单位长度可得C点坐标,进而可得A点坐标,然后再由条件AB=AC可得p=4,进而可确定B点坐标;
②根据三角形的面积公式可得三角形ABC的面积.
解答 解:(1)∵点A(2,n)在第一象限,把点A向右移p个单位长度得点B,
∴B(2+p,n);
(2)①点A向下平移4个单位长度得到点C(2,n-4),
∵点C距x轴1个单位长度,
∴|n-4|=1,
n=5或3,
当n=5时,C(2,1),则A(2,5),
当n=3时,C(2,1),则A(2,3),
∵AB=AC,
∴p=4,
∴B(6,5)或(6,3);
②三角形ABC的面积:4×4×$\frac{1}{2}$=8.
点评 此题主要考查了点坐标,以及图形的平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.

练习册系列答案
相关题目
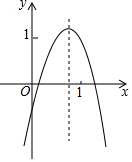 已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a-b中,其值为正的式子的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a-b中,其值为正的式子的个数是( ) 如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.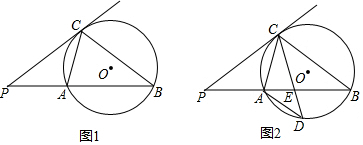

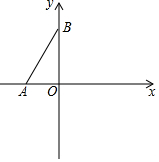 如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.
如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.