题目内容
9.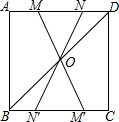 如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.
如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.(1)求证:MN=M′N′;
(2)在不添加其他辅助线的情况下,直接写出图中的所有的全等三角形.
分析 (1)根据正方形的性质得到AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,根据全等三角形的性质得到OM=OM′,MN=M′N′;
(2)根据全等三角形的判定定理可以判断△ABD≌△BCD,△MDO≌△M′BO,△NOD≌△N′OB,△MON≌△M′ON′.由此即可得出答案.
解答 解: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,
∴∠MDO=∠M′BO,
在△MOD和△M′OB中,$\left\{\begin{array}{l}{∠MDO=∠M′BO}\\{∠MOD=∠M′OB}\\{DM=BM′}\end{array}\right.$,
∴△MDO≌△M′BO,
∴OM=OM′,
∵AD∥BC,
∴∠DMO=∠BM′O,
在△MON与△M′ON′中$\left\{\begin{array}{l}{∠NMO=∠N′M′O}\\{OM=OM′}\\{∠MON=∠M′ON′}\end{array}\right.$,
∴△MON≌△M′ON′,
∴MN=M′N′;
(2)∵四边形ABCD是正方形,
∴AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,
∴∠MDO=∠M′BO,
在△MOD和△M′OB中,$\left\{\begin{array}{l}{∠MDO=∠M′BO}\\{∠MOD=∠M′OB}\\{DM=BM′}\end{array}\right.$,
∴△MDO≌△M′BO,
∴OM=OM′,
∵AD∥BC,
∴∠DMO=∠BM′O,
在△MON与△M′ON′中$\left\{\begin{array}{l}{∠NMO=∠N′M′O}\\{OM=OM′}\\{∠MON=∠M′ON′}\end{array}\right.$,
∴△MON≌△M′ON′,
∴MN=M′N′;
同理△NOD≌△N′OB,
在△ABD和△BCD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠C}\\{AD=CD}\end{array}\right.$,
∴△ABD≌△BCD,
∴全等三角形一共有△MDO≌△M′BO,△MON≌△M′ON′,△NOD≌△N′OB,△ABD≌△BCD4对.
点评 本题考查正方形的性质、全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定方法,属于基础题,中考常考题型.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案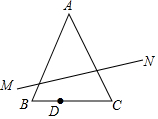 如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是3.
如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是3.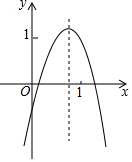 已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a-b中,其值为正的式子的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a-b中,其值为正的式子的个数是( ) 如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.