题目内容
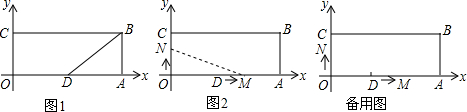
9.如图,已知双曲线y=$\frac{2}{x}$与直线y=x相交于A,B两点,点C(2,2),D(-2,-2)在直线y=x上.(1)若点P(1,m)为双曲线y=$\frac{2}{x}$上一点,求PD-PC的值.
(2)若点P(x,y)(x>0)为双曲线y=$\frac{2}{x}$上一动点,请问PD-PC的值是否为定值?请说明理由.
(3)若点P(x,y)(x>0)为双曲线y=$\frac{2}{x}$上一动点,连接PC交双曲线另一点E,当点P(x,y)使得PD-CE=2PC.求P的坐标.

分析 (1)把P坐标代入双曲线解析式求出m的值,确定出P的坐标,利用两点间的距离公式求出PD与PC的长,即可求出PD-PC的值;
(2)PD-PC的值为定值,理由为:把P坐标代入双曲线解析式表示出y,利用两点间的距离公式表示出PD与PC,求出之差即可;
(3)由对称性得到P与E关于y=x对称,即PC=CE=$\frac{1}{2}$PE,要使PD-PC=2PC,即PD=3PC,由(2)表示出的PD与PC,列出关于x的方程,求出方程的解得到x的值,即可确定出P坐标.
解答 解:(1)把P(1,m)代入双曲线解析式得:m=2,即P(1,2),
∵C(2,2),D(-2,-2),
∴PD=$\sqrt{(1+2)^{2}+(2+2)^{2}}$=5,PC=$\sqrt{(1-2)^{2}+(2-2)^{2}}$=1,
则PD-PC=5-1=4;
(2)PD-PC的值为定值4,理由为:
把P(x,y)代入双曲线解析式得:y=$\frac{2}{x}$,即P(x,$\frac{2}{x}$),
∵C(2,2),D(-2,-2),x>0,
∴x+$\frac{2}{x}$≥2$\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$>2,
∴PD=$\sqrt{(x+2)^{2}+(\frac{2}{x}+2)^{2}}$=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}+4x+\frac{8}{x}+8}$=$\sqrt{(x+\frac{2}{x})^{2}+4(x+\frac{2}{x})+4}$=$\sqrt{(x+\frac{2}{x}+2)^{2}}$=x+$\frac{2}{x}$+2,
PC=$\sqrt{(x-2)^{2}+(\frac{2}{x}-2)^{2}}$=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}-4x-\frac{8}{x}+8}$=$\sqrt{(x+\frac{2}{x})^{2}-4(x+\frac{2}{x})+4}$=x+$\frac{2}{x}$-2,
则PD-PC=x+$\frac{2}{x}$+2-x-$\frac{2}{x}$+2=4;
(3)由对称性可得P与E关于y=x对称,即PC=CE=$\frac{1}{2}$PE,
∵P(x,y),∴E(y,x),
把P(x,y)代入反比例解析式得:y=$\frac{2}{x}$,即P(x,$\frac{2}{x}$),E($\frac{2}{x}$,x),
要使PD-CE=2PC,即PD=3PC,
由(2)得:x+$\frac{2}{x}$+2=3(x+$\frac{2}{x}$-2),
整理得:x2-4x+2=0,
解得:x=$\frac{4±2\sqrt{2}}{2}$=2±$\sqrt{2}$,
当x=2+$\sqrt{2}$时,P坐标为(2+$\sqrt{2}$,2-$\sqrt{2}$);当x=2-$\sqrt{2}$时,P坐标为(2-$\sqrt{2}$,2+$\sqrt{2}$).
点评 此题考查了一次函数与反比例函数的交点,熟练掌握两点间的距离公式是解本题的关键.

 期末集结号系列答案
期末集结号系列答案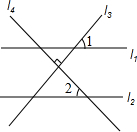 如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )| A. | 46° | B. | 44° | C. | 23° | D. | 22° |
| A. | x<2 | B. | x<-2 | C. | x>-2 | D. | x>2 |