题目内容
6.某电信局收取网费如下:163网费为每小时3元;169网费为每小时2元,但要收取15元月租费.设网费为y(元),上网时间为x(时).分别写出y与x的函数关系式,某网民每月上网19小时,他应选那种上网方式.分析 (1)y1=每小时收费额×小时数,y2=每小时收费额×小时数+月租费;
(2)分别求出y1<y2,y1=y2,y1>y2时x的取值范围,根据x的取值范围即可选择入网的方式.
解答 解:(1)根据题意,得:
163网费为:y1=3x(x>0),
169网费为:y2=2x+15(x>0);
(2)当y1<y2时,3x<2x+15,解得x<15;
当y1=y2时,3x=2x+15,解得x=15;
当y1>y2时,3x>2x+15,解得x>15.
综上所述:当该用户上网时间少于15小时时,选择163网省钱;
当上网时间等于15小时时选择163、169费用一样;
当上网时间超过15小时时选择169网省钱.
点评 本题考查了一次函数的应用,难度中等.得到两种上网方式的关系式是解决本题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
16.下列各对数中,互为相反数的一对数是( )
| A. | -23与-32 | B. | (-2)3与-23 | C. | (-3)2与-32 | D. | -(-1)与1 |
14.已知0.8622=0.7396,若x2=0.7396,则x的值等于( )
| A. | 0.862 | B. | -0.862 | C. | ±0.862 | D. | ±8.62 |
15.以下列各组数为边长,能构成直角三角形的是( )
| A. | 12,15,20 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 0.3,0.4,0.5 | D. | 32,42,52 |
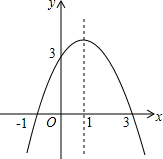 抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3). 如图,AD垂直平分BC,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=116°,则∠ABC的度数为52°.
如图,AD垂直平分BC,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=116°,则∠ABC的度数为52°.
