题目内容
18.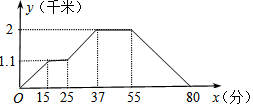 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )| A. | 1.1,0.08 | B. | 1.1,0.025 | C. | 0.9,0.08 | D. | 0.9,0.025 |
分析 根据观察图象的纵坐标,可得菜地与玉米地的距离;根据观察图象的横坐标,可得再浇水时间、除草时间,根据有理数的减法,可得答案.
解答 解;由纵坐标看出家到菜地的距离是1.1千米,家到玉米地的距离是2千米,菜地和玉米地的距离为:2-1.1=0.9千米;
由横坐标看出小强从玉米地回家的时间为80-55=25(分钟),
家到玉米地的距离是2千米,小强从玉米地回家的平均速度为2÷25=0.08千米/分钟,
故选C.
点评 本题考查了函数图象,观察函数图象的坐标是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如表(为所学过的一次函数,反比例函数或二次函数中的一种).
(1)请求出每亩获得利润y与x的函数关系式,并写出自变量的取值范围;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过60亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
| x(亩) | 20 | 25 | 30 | 35 |
| y(元) | 1800 | 1700 | 1600 | 1500 |
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过60亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
13.下列关于$\sqrt{5}$的叙述,错误的是( )
| A. | $\sqrt{5}$是有理数 | B. | 面积为5的正方形边长是$\sqrt{5}$ | ||
| C. | $\sqrt{5}$介于2和3之间 | D. | 在数轴上可以找到表示$\sqrt{5}$的点 |
10.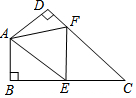 在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )
在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )
 在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )
在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )| A. | 55° | B. | 70° | C. | 125° | D. | 110° |
 请将下列解答过程补充完整.
请将下列解答过程补充完整.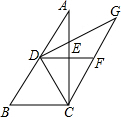 如图,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延长线于点F.
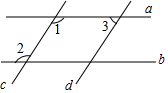
如图,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延长线于点F. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )



 如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.
如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.