题目内容
8. 如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.
如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.(1)求证:AF=DE;
(2)若AC═6,BC=10,求四边形AEDF的周长.
分析 (1)根据三角形中位线定理、直角三角形的性质证明四边形DEAF是平行四边形,根据平行四边形的性质证明;
(2)由(1)的结论计算即可.
解答 (1)证明:∵D,E分别为AB,BC的中点,
∴DE∥AC,DE=$\frac{1}{2}$AC,
∵∠BAC=90°,E为BC的中点,
∴EA=EB,
∴∠EAB=∠B,又∠FDA=∠B,
∴∠FDA=∠EAB,
∴EA∥DF,
∴四边形DEAF是平行四边形,
∴AF=DE;
(2)解:∵∠BAC=90°,E为BC的中点,
∴EA=$\frac{1}{2}$BC=5,
∵D,E分别为AB,BC的中点,
∴DE=$\frac{1}{2}$AC=3,
∴四边形AEDF的周长=2×(3+5)=16.
点评 本题考查的是三角形中位线定理的应用、平行四边形的判定,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
18.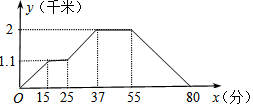 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )| A. | 1.1,0.08 | B. | 1.1,0.025 | C. | 0.9,0.08 | D. | 0.9,0.025 |
19. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )| A. | 美 | B. | 丽 | C. | 资 | D. | 中 |
 如图,AB∥ED,已知AC=BE,且点B、C、D三点共线,若∠E=∠ACB.求证:BC=DE.
如图,AB∥ED,已知AC=BE,且点B、C、D三点共线,若∠E=∠ACB.求证:BC=DE.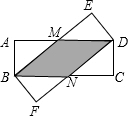 如图,已知四边形ABCD、四边形DEBF都是矩形,AB=BF,BE,AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形.
如图,已知四边形ABCD、四边形DEBF都是矩形,AB=BF,BE,AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形.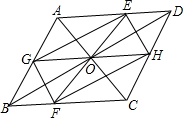 已知:如图,在?ABCD中,对角线AC、BD相交于点O,直线EF过点O,分别交AD、BC于点E、F,直线GH过点O,分别交AB,CD于点G、H.求证:四边形EGFH是平行四边形.
已知:如图,在?ABCD中,对角线AC、BD相交于点O,直线EF过点O,分别交AD、BC于点E、F,直线GH过点O,分别交AB,CD于点G、H.求证:四边形EGFH是平行四边形.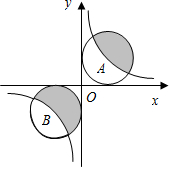 如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π.
如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π.