题目内容
10.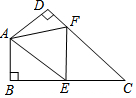 在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )
在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )| A. | 55° | B. | 70° | C. | 125° | D. | 110° |
分析 要使△AEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′E+∠A″=∠HAA′=55°,进而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.
解答 解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,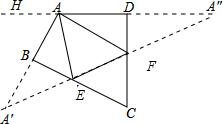
∵∠C=55°,
∴∠DAB=125°,
∴∠HAA′=55°,
∴∠AA′E+∠A″=∠HAA′=55°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=55°,
∴∠EAF=125°-55°=70°.
故选B.
点评 本题考查的是轴对称-最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出E,F的位置是解题关键.

练习册系列答案
相关题目
10.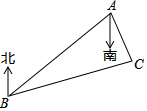 如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )
 如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )| A. | 95° | B. | 85° | C. | 60° | D. | 40° |
1. 下列图形中有可能与图相似的是( )
下列图形中有可能与图相似的是( )
 下列图形中有可能与图相似的是( )
下列图形中有可能与图相似的是( )| A. |  | B. |  | C. |  | D. |  |
18.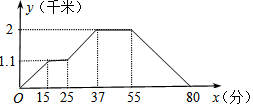 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )| A. | 1.1,0.08 | B. | 1.1,0.025 | C. | 0.9,0.08 | D. | 0.9,0.025 |
5.小明统计了他家今年11月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15min的频率为( )
| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 19 | 16 | 5 | 10 |
| A. | 0.1 | B. | 0.4 | C. | 0.5 | D. | 0.8 |
2.下列计算正确的是( )
| A. | (-a3)2=-a6 | B. | 9a3÷3a3=3a3 | C. | 2a3+3a3=5a6 | D. | 2a3•3a2=6a5 |
19. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )| A. | 美 | B. | 丽 | C. | 资 | D. | 中 |