题目内容
17.关于x、y的两个方程组$\left\{\begin{array}{l}{ax-2by=2}\\{2x-y=7}\end{array}\right.$和$\left\{\begin{array}{l}{3ax-5by=9}\\{3x-y=11}\end{array}\right.$具有相同的解,则a、b的值是多少?分析 根据方程组的解相同,可得只含有x、y的方程组,根据解方程组,可得x、y的值,根据方程组的解满足方程组,可得关于a、b的方程组,根据代入消元法,可得答案.
解答 解:联立$\left\{\begin{array}{l}{2x-y=7①}\\{3x-y=11②}\end{array}\right.$,
②-①,得
x=4,
把x=4代入①,得8-y=7,解得y=1,
方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
将$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$代入$\left\{\begin{array}{l}{4a-2b=2}\\{12a-6b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$.
点评 本题考查了二元一次方程组的解,将x、y的值代入得出关于a、b的方程组是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.一个直角三角形的直角边长分别为3和5,第三边的长是方程x2-6x+8=0的根,则这个三角形的周长为( )
| A. | 10 | B. | 12 | C. | 10或12 | D. | 以上都不对 |
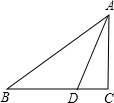 如图,△ABC中∠C=90°,点D在BC上,且DB=DA,tan∠DAC=$\frac{1}{2}$,则tanB=$\frac{\sqrt{5}-1}{2}$.
如图,△ABC中∠C=90°,点D在BC上,且DB=DA,tan∠DAC=$\frac{1}{2}$,则tanB=$\frac{\sqrt{5}-1}{2}$.