题目内容
12．不等式组$\left\{\begin{array}{l}{3（x-1）＜-6}\\{\frac{3-x}{2}≤1}\end{array}\right.$的解集是（ ）| A． | x≥1 | B． | -1＜x＜1 | C． | x＜-1 | D． | 无解 |
分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：解不等式3（x-1）＜-6，得：x＜-1，
解不等式$\frac{3-x}{2}$≤1，得：x≥1，
则不等式组无解，
故选：D．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
20．
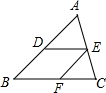如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，若DE∥BC，EF∥AB，则下面所列比例式中正确的是（ ）
如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，若DE∥BC，EF∥AB，则下面所列比例式中正确的是（ ）| A． | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B． | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C． | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D． | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
12．若将△ABC沿射线OT方向平移一段距离后与△DEF完全重合，则①AD=BE=CF；②AD∥BE∥CF；③AB=DE，AC=DF，BC=EF；④AB∥DE，AC∥DF，BC∥EF中一定成立的是（ ）
| A． | ②④ | B． | ①③ | C． | ①③④ | D． | ①②③④ |
13．关于三角形的三条高，下列说法正确的是（ ）
| A． | 三条高都在三角形的内部 | B． | 三条高都在三角形的外部 | ||
| C． | 至多有一条在三角形的内部 | D． | 至少有一条在三角形的内部 |