��Ŀ����
13�� ��ͼ��Rt��ABC�У���B=90�㣬AB=3cm��BC=4cm����D��AC�ϣ�AD=1cm����P�ӵ�A��������AB�����˶�����Q�ӵ�C��������C��B��A��C��·�������˶�������ͬʱ��������B�㴦�״�������P���˶��ٶ�ÿ�������2cm������B��C��A��·�������˶�����Q�����ٶȲ��䣬��������ԭ·�������˶���������D�㴦�ٴ�������ֹͣ�˶������Pԭ�����ٶ�Ϊxcm/s��
��ͼ��Rt��ABC�У���B=90�㣬AB=3cm��BC=4cm����D��AC�ϣ�AD=1cm����P�ӵ�A��������AB�����˶�����Q�ӵ�C��������C��B��A��C��·�������˶�������ͬʱ��������B�㴦�״�������P���˶��ٶ�ÿ�������2cm������B��C��A��·�������˶�����Q�����ٶȲ��䣬��������ԭ·�������˶���������D�㴦�ٴ�������ֹͣ�˶������Pԭ�����ٶ�Ϊxcm/s����1����Q���ٶ�Ϊ$\frac{4}{3}$xcm/s���ú�x�Ĵ���ʽ��ʾ����
��2�����Pԭ�����ٶȣ�
���� ��1�����Q���ٶ�Ϊycm/s����������÷��̼��ɵõ����ۣ�
��2�����ݹ��ɶ����õ�AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5�����CD=5-1=4���з��̼��ɵõ����ۣ�
��� �⣺��1�����Q���ٶ�Ϊycm/s��
�������3��x=4��y��
��y=$\frac{4}{3}$x��
�ʴ�Ϊ��$\frac{4}{3}$x��
��2��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5��
CD=5-1=4��
��B�㴦�״�������P���˶��ٶ�Ϊ��x+2��cm/s��
�������$\frac{3+1}{\frac{4x}{3}}$=$\frac{4+4}{x+2}$��
��ã�x=$\frac{6}{5}$��cm/s����
�𣺵�Pԭ�����ٶ�Ϊ$\frac{6}{5}$cm/s��
���� ���⿼���˷�ʽ���̵�Ӧ�ã����ɶ�������ȷ�����������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
�����Ŀ
6��������ʽ����ƽ���ʽ������ǣ�������
| A�� | ��2a+b����2b-a�� | B�� | ��a+1����-a-1�� | C�� | ��3x-y����-3x+y�� | D�� | ��-m-n����-m+n�� |
5��Rt��ABC�У���B=90�㣬AB=3��BC=4��BD��AC�������ߣ�BH��AC���ϸߣ���BD��BH��ֵ�ֱ��ǣ�������
| A�� | 5��2.4 | B�� | 2.5��$\sqrt{7}$ | C�� | 2.5��2.5 | D�� | 2.5��2.4 |
8�����ж���ʽ�У������ù�ʽ���зֽ���ʽ���ǣ�������
| A�� | a2+b2 | B�� | m-n2 | C�� | x2-9 | D�� | x2+2xy-y2�� |
18��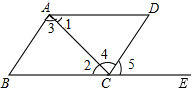 ��ͼ����E��BC���ӳ����ϣ��������������ж�AB��CD���ǣ�������
��ͼ����E��BC���ӳ����ϣ��������������ж�AB��CD���ǣ�������
 ��ͼ����E��BC���ӳ����ϣ��������������ж�AB��CD���ǣ�������
��ͼ����E��BC���ӳ����ϣ��������������ж�AB��CD���ǣ�������| A�� | ��1=��2 | B�� | ��3=��4 | C�� | ��D+��BCD=180�� | D�� | ��D=��5 |
5�����㣨-2��99+��-2��100�Ľ��Ϊ��������
| A�� | 299 | B�� | 2100 | C�� | -299 | D�� | -2 |
2����֪����ABCD�ĶԽ��ߵij��ȷֱ�Ϊ6��8��������ABCD���ܳ�Ϊ��������
| A�� | 5 | B�� | 10 | C�� | 20 | D�� | 40 |
20����֪��Rt��ABC�У���C=90�㣬��A=����AC=2����ôAB�ij�Ϊ��������
| A�� | 2sin�� | B�� | 2cos�� | C�� | $\frac{2}{sin��}$ | D�� | $\frac{2}{cos��}$ |
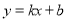 ��
��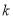 ��
�� ������
Ϊ������ 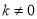 ��ͼ����ͼ��ʾ�������
��ͼ����ͼ��ʾ�������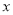 �IJ���ʽ
�IJ���ʽ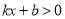 �Ľ⼯Ϊ�� ��
�Ľ⼯Ϊ�� ��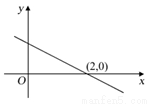
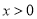 B.
B. 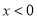 C.
C. 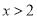 D.
D.