题目内容
12.命题“有一条边和一个锐角分别相等的两个直角三角形全等”是假命题.(填“真”或“假”)分析 根据直角三角形全等的判定方法判断即可.
解答  解:一条边和一个锐角分别相等的两个直角三角形,边与角不一定是对应边和对应角,
解:一条边和一个锐角分别相等的两个直角三角形,边与角不一定是对应边和对应角,
例如:两个直角三角形中相等的∠α的邻边与对边相等,两个三角形不全等,
所以,这两个直角三角形不一定全等,
所以,“有一条边和一个锐角分别相等的两个直角三角形全等”是假命题.
故答案为:假.
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
2.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,设每次降价的百分率为x,则下面所列的方程中正确的是( )
| A. | 560(1-x)2=315 | B. | 560(1+x)2=315 | C. | 560(1-2x)2=315 | D. | 560(1-x2)=315 |
3.若多项式x2+mx+12因式分解的结果是(x-2)(x-6),则m的值是( )
| A. | 8 | B. | -4 | C. | -8 | D. | 4 |
7.如图(1)是长方形纸片,∠DAC=20°将纸片沿AC折叠成图(2),再沿EC折叠成图(3),则图(3)中∠ACD为( )


| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
4.将抛物线y=x2向上平移1个单位,得到的抛物线解析式为( )
| A. | y=(x-1)2 | B. | y=x2-1 | C. | y=(x+1)2 | D. | y=x2+1 |
1. 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )| A. | -3<x<2 | B. | -3<x<0或x>2 | C. | x>-3 | D. | x<2 |
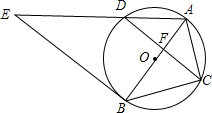 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.