题目内容
一个自然数m，若将其数字重新排列可得一个新的自然数n，如果m=3n，我们称m是一个“希望数”．例如：3105=3×1035，71253=3×23751，371250=3×123750．
（1）请说明41不是希望数，并证明任意两位数都不可能是“希望数”．
（2）一个四位“希望数”M记为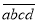
，已知
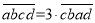，且c=2，请求出这个四位“希望数”．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
口算题卡北京妇女儿童出版社系列答案题目内容
一个自然数m，若将其数字重新排列可得一个新的自然数n，如果m=3n，我们称m是一个“希望数”．例如：3105=3×1035，71253=3×23751，371250=3×123750．
（1）请说明41不是希望数，并证明任意两位数都不可能是“希望数”．
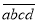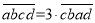（2）一个四位“希望数”M记为，已知，且c=2，请求出这个四位“希望数”．
口算题卡北京妇女儿童出版社系列答案
，得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”(a≠0且a≠1)，能否求出1＋a＋a2＋a3＋a4＋…＋a2016的值？你的答案是（ ）
B. 
C. 
D. 
a2+ab+
b2=________．
（a＞0）
=___________．