题目内容
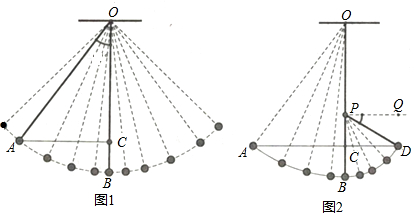
10.如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.(取sin37°=0.6,cos37°=0.8,tan37°=0.75)(1)求点A与点B的高度差BC的值.
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度.
分析 (1)根据题意得出CB=OB-OC=OB-OAcos37°,进而得出答案;
(2)根据题意得出BP=BP-CP=PD-PD•cos60°=10,进而得出PB的长,进而得出答案.
解答 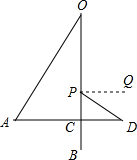 解:(1)∵AD⊥OB,
解:(1)∵AD⊥OB,
由题意可得:∠AOB=37°,
则CB=OB-OC=OB-OAcos37°=50-50×0.8=10(cm),
故A,B之间的高度差BC为10cm;
(2)由(1)知,B,D的高度差也是10cm,
故BC=BP-CP=PD-PD•cos60°=10(cm),
解得:PB=20,
则OP=OB-BC=50-20=30(cm).
答:OP这段细绳的长度为30cm.
点评 此题主要考查了解直角三角形的应用,根据题意得出OC与OA的关系是解题关键.

练习册系列答案
相关题目
1.如果一个角的补角是130°,那么这个角的余角的度数是( )
| A. | 30° | B. | 40° | C. | 50° | D. | 90° |
5.方程$\frac{2}{x}=\frac{3}{x-1}$的解为( )
| A. | x=-2 | B. | x=2 | C. | x=-1 | D. | x=$\frac{1}{2}$ |
2.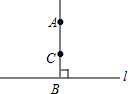 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点能作一条垂线 | |
| D. | 垂线段最短 |
20.已知a+$\frac{1}{a}$=$\sqrt{7}$,则a-$\frac{1}{a}$的值为( )
| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
 如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.