题目内容
19. 如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.(1)当t为多少时,以点ABQD为顶点的四边形是平行四边形?
(2)当t为多少时,以点ABQP为顶点的四边形是平行四边形?
分析 (1)当四边形ABQD为平行四边形时,AD=BQ=8,由题意得出方程,解方程即可;
(2)当四边形ABQP为平行四边形时,AP=BQ; 由题意得出方程,解方程即可.
解答 解:(1)∵当四边形ABQD为平行四边形时,AD=BQ=8,
又∵Q点速度为2个单位/秒,
∴16-2t=8,
解得:t=4,
即当t为4秒时,以点ABQD为顶点的四边形是平行四边形;
(2)∵当四边形ABQP为平行四边形时,AP=BQ;
又∵点P、Q速度分别为1个单位/秒、2个单位/秒,AD=8,BC=16,
∴t=16-2t,
解得:t=$\frac{16}{3}$,
即当t为$\frac{16}{3}$秒时,以点ABQP为顶点的四边形是平行四边形.
点评 本题考查了平行四边形的判定;熟记平行四边形的判定方法,由题意得出方程是解决问题的关键.

练习册系列答案
相关题目
9.代数式:2mn,3a2-1,-$\frac{2}{9}$x,8,$\frac{ab}{π}$中,单项式共有( )个.
| A. | 2个 | B. | B3个 | C. | 4个 | D. | 5个 |
14.能确定四边形是平行四边形的条件的是( )
| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组邻角相等 | ||
| C. | 一组对边平行且相等 | D. | 两条对角线相等 |


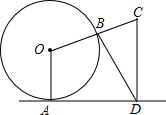 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.