题目内容
5.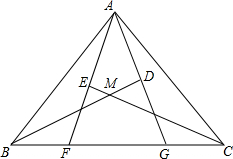 如图,△AFG中,BD、CE分别为AG、AF边的中垂线,交直线FG于点B、C,BD、CE交于点M,联结AB、AC,已知∠BAF=38°,∠CAG=22°,求∠BMC.
如图,△AFG中,BD、CE分别为AG、AF边的中垂线,交直线FG于点B、C,BD、CE交于点M,联结AB、AC,已知∠BAF=38°,∠CAG=22°,求∠BMC.
分析 设∠FAG=x,根据线段的垂直平分线的性质得到BA=BG,CA=CF,根据等腰三角形的性质用x表示出∠BGA和∠CFA,根据三角形内角和定理列式计算即可.
解答 解:设∠FAG=x,
∵BD、CE分别为AG、AF边的中垂线,
∴BA=BG,CA=CF,
∴∠BGA=∠BAG=x+38°,∠CFA=∠CAF=x+22°,
∴x+x+38°+x+22°=180°,
解得,x=40°,
则∠BMC=360°-90°-90°-40°=140°.
点评 本题考查的是线段的垂直平分线的性质和三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等、运用方程思想是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
13.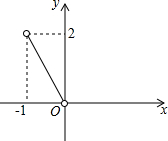 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )
 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )| A. | y=-2x | B. | y=-2x(-1<x<0) | C. | y=-$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x(-1<x<0) |
 如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,并且BE=CF,求证:点D在BC的垂直平分线上.
如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,并且BE=CF,求证:点D在BC的垂直平分线上. 如图所示,AB=AC=12,BC=7,AB的垂直平分线交AB于D,交AC于F,求△BCE的周长.
如图所示,AB=AC=12,BC=7,AB的垂直平分线交AB于D,交AC于F,求△BCE的周长. 如图,在a上找到M、N两点,且MN=10mm,M在N的左边,使四边形ABMN的周长最短.
如图,在a上找到M、N两点,且MN=10mm,M在N的左边,使四边形ABMN的周长最短.