题目内容
10.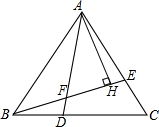 已知等边三角形ABC中,D、E是BC、AC边上的点,BD=CE,AD与BE相交于点F,AH⊥BE于H.若FH=5,求AF的长度.
已知等边三角形ABC中,D、E是BC、AC边上的点,BD=CE,AD与BE相交于点F,AH⊥BE于H.若FH=5,求AF的长度.
分析 证△ABD≌△CBE,推出∠BAD=∠CBE,求出∠AFH=∠ABD=60°,得出∠FAH=30°,根据含30度角的直角三角形性质求出即可.
解答 解:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
在△ABD和△CBE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABD=∠BCE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠CBE,
∴∠AFH=∠ABF+∠BAF=∠ABF+∠CBE=∠ABC=60°,
∵AH⊥BE,
∴∠FAH=30°,
在Rt△AFH中,∠FAH=30°,
∴AF=2FH,
∵FH=5,
∴AF=10.
点评 本题考查了等边三角形性质,全等三角形的性质和判定,三角形外角性质,含30度角的直角三角形性质的应用,关键是求出∠FAH=30°.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,利用关于坐标轴对称的点的坐标特点,画出△ABC关于x轴或y轴对称的图形.
如图,利用关于坐标轴对称的点的坐标特点,画出△ABC关于x轴或y轴对称的图形. 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.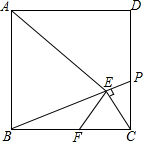 正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F
正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F  如图,△ABC中,D、E、F、G分别在边上,且DE∥GF,已知BE=DE,CF=FG,求∠A的度数.
如图,△ABC中,D、E、F、G分别在边上,且DE∥GF,已知BE=DE,CF=FG,求∠A的度数.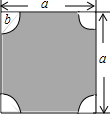 如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.
如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.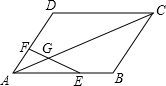 如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.
如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.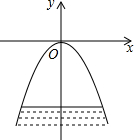 如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.
如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.