题目内容
15．
如图，△ABC中，D、E、F、G分别在边上，且DE∥GF，已知BE=DE，CF=FG，求∠A的度数．
分析 由题中条件可得∠B=∠BDE，∠C=∠CGF，进而再利用外角的性质及平行线的性质，即可得出结论．
解答 解：∵BE=DE，CF=FG，
∴∠B=∠BDE，∠C=∠CGF，
∠DEF=∠B+∠BDE=2∠B，则∠EFG=2∠C，
∵DE∥GF，
∴∠DEF+∠EFG=180°，
∴$\frac{1}{2}$（∠DEF+∠EFG）=∠B+∠C=90°，
∴∠A=90°．
点评 本题考查了等腰三角形的性质，平行线的性质以及三角形的内角和定理，熟练掌握等腰三角形的性质是解题的关键．
练习册系列答案
相关题目
5．下列方程中一定是一元二次方程的是（ ）
| A． | x2=0 | B． | x+$\frac{1}{3-x}$-2x2=0 | C． | ax2+bx+c=0 | D． | x2+2y+3=0 |
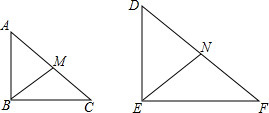如图，Rt△ABC∽Rt△DEF，且DE=2AB，BM，EN是斜边上的中线
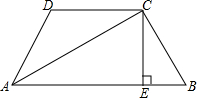如图，已知在四边形ABCD中．∠B+∠D=180°，AC平分∠BAD，CE⊥AB，E为垂足．求证：AB+AD=2AE．
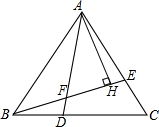已知等边三角形ABC中，D、E是BC、AC边上的点，BD=CE，AD与BE相交于点F，AH⊥BE于H．若FH=5，求AF的长度．
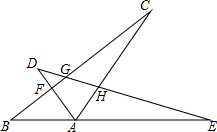如图，在△ABC中，∠BAC=120°，将△ABC绕点A顺时针旋转60°得△ADE，则图中有3对全等三角形，它们是△ADE≌△ABC，BAF≌△DAH，△AEH≌△ACF．
如图，在平面直角坐标系xOy中，点M为抛物线y=-x2+2nx-n2+2n（n＞2）的顶点，直线y=-$\frac{1}{2}$x与抛物线交于点P、Q，过点P作PA∥x轴，交抛物线于另一点A，交y轴于点B．