题目内容
18. 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.(1)在图中画出点M,N,写出点M,N的坐标并指出点K所在的位置;
(2)求经过第2014次跳动之后,棋子落点与点P之间的距离.
分析 (1)利用中心对称的性质和网格特征分别画出点M、N、K,然后写出M、N的坐标,同时可判断K点位置;
(2)由(1)得棋子从点P开始跳动,每三次一循环,而2014=3×671+1,所以经过第2014次跳动之后棋子落在点M处,然后利用勾股定理计算PM.
解答 解:(1)如图,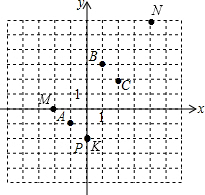
M(-2,0),N(4,6);K点与P点重合;
(2)因为2014=3×671+1,
所以经过第2014次跳动之后,棋子落在M点处,MP=2$\sqrt{2}$.
点评 本题考查了坐标与图形变化:旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 已知AB∥CD,BD平分∠ABC,DB平分∠ADC,求证:DA∥BC.
已知AB∥CD,BD平分∠ABC,DB平分∠ADC,求证:DA∥BC.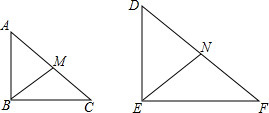 如图,Rt△ABC∽Rt△DEF,且DE=2AB,BM,EN是斜边上的中线
如图,Rt△ABC∽Rt△DEF,且DE=2AB,BM,EN是斜边上的中线 测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题
测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题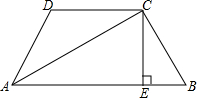 如图,已知在四边形ABCD中.∠B+∠D=180°,AC平分∠BAD,CE⊥AB,E为垂足.求证:AB+AD=2AE.
如图,已知在四边形ABCD中.∠B+∠D=180°,AC平分∠BAD,CE⊥AB,E为垂足.求证:AB+AD=2AE.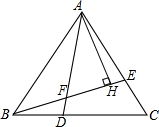 已知等边三角形ABC中,D、E是BC、AC边上的点,BD=CE,AD与BE相交于点F,AH⊥BE于H.若FH=5,求AF的长度.
已知等边三角形ABC中,D、E是BC、AC边上的点,BD=CE,AD与BE相交于点F,AH⊥BE于H.若FH=5,求AF的长度. 如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.
如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B. △ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )