题目内容
16.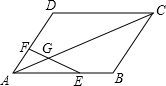 如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.
如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.
分析 首先求证出EO∥BC,得到EO=$\frac{1}{2}$BC,然后根据平行线的性质求证出△AFG∽△OEG.进而得到$\frac{AG}{OG}=\frac{AF}{OE}$,因为AF:AD=1:3,AD=BC,等量代换即可得到结论.
解答 解:设AC的中点为O,连接EO,又E是AB的中点,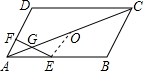
∴EO∥BC,EO=$\frac{1}{2}$BC,
∵AD∥BC,
∴AF∥EO,
∴△AFG∽△OEG,
∴$\frac{AG}{OG}=\frac{AF}{OE}$,
∵AF:FD=1:2,
AD=BC,
∴AF:BC=$\frac{1}{3}$,
∴$\frac{AG}{OG}$=$\frac{\frac{1}{3}}{\frac{1}{2}}$=$\frac{2}{3}$,
∴$\frac{AG}{GC}$=$\frac{1}{4}$.
点评 此题主要考查相似三角形的判定和性质,平行线分线段成比例定理,能综合利用平行线分线段成比例、平行线的性质、比例的性质是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.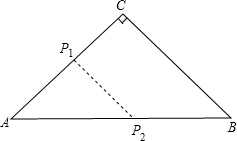 如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )
如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )
 如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )
如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )| A. | S=t(100-t) | B. | S=$\frac{\sqrt{2}}{2}{t}^{2}-5\sqrt{2}t$ | C. | S=$\frac{\sqrt{2}}{2}{t}^{2}$ | D. | S=-$\frac{\sqrt{2}}{4}{t}^{2}+25\sqrt{2}t$ |
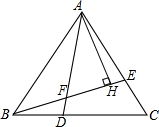 已知等边三角形ABC中,D、E是BC、AC边上的点,BD=CE,AD与BE相交于点F,AH⊥BE于H.若FH=5,求AF的长度.
已知等边三角形ABC中,D、E是BC、AC边上的点,BD=CE,AD与BE相交于点F,AH⊥BE于H.若FH=5,求AF的长度. 如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.
如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B. △ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )