题目内容
11.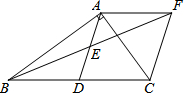 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
分析 (1)根据AAS证△AFE≌△DBE;
(2)利用全等三角形的对应边相等得到AF=BD.证出四边形ADCF是平行四边形,再由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
解答 (1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AEF和△DEB中,$\left\{\begin{array}{l}{∠AFE=∠DBE}&{\;}\\{∠FEA=∠BED}&{\;}\\{AE=DE}&{\;}\end{array}\right.$,
∴△AEF≌△DEB(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=$\frac{1}{2}$BC,
∴四边形ADCF是菱形;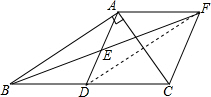 (3)解:连接DF,如图所示:
(3)解:连接DF,如图所示:
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=4,
∵四边形ADCF是菱形,
∴菱形ADCF的面积=$\frac{1}{2}$AC?DF=$\frac{1}{2}$×3×4=6.
点评 本题考查了全等三角形的性质和判定,平行四边形的判定,菱形的判定的应用,菱形的面积计算;熟练掌握菱形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
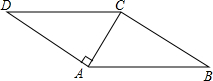 如图,在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是4$\sqrt{3}$+8.
如图,在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是4$\sqrt{3}$+8. 如图为实数a,b在数轴上的位置,则($\sqrt{b}$)2+$\sqrt{(-a)^{2}}$-$\sqrt{(a-b)^{2}}$=0.
如图为实数a,b在数轴上的位置,则($\sqrt{b}$)2+$\sqrt{(-a)^{2}}$-$\sqrt{(a-b)^{2}}$=0.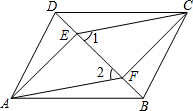 如图,在?ABCD中,AE∥CF,求证:∠1=∠2.
如图,在?ABCD中,AE∥CF,求证:∠1=∠2.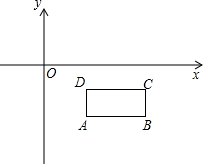 如图,已知矩形ABCD四个顶点的坐标分别是A(2,$-2\sqrt{2}$),B(5,$-2\sqrt{2}$),C(5,$-\sqrt{2}$),D(2,$-\sqrt{2}$)
如图,已知矩形ABCD四个顶点的坐标分别是A(2,$-2\sqrt{2}$),B(5,$-2\sqrt{2}$),C(5,$-\sqrt{2}$),D(2,$-\sqrt{2}$)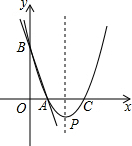 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.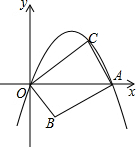 如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.